Aufgabe:
Satz von Taylor auf Funktion anwenden
Problem/Ansatz:
Gegeben ist folgende Funktion (Foto 1)
Außerdem noch ihre Ableitungen (Foto 2)
Darauf soll nun der Satz von Taylor angewendet werden, welcher wie folgt formuliert wurde (Foto 3)
Und genau das verstehe ich nicht. Warum muss n größer x^2 sein? Es wäre doch sicherlich denkbar das n anders zu wählen, oder?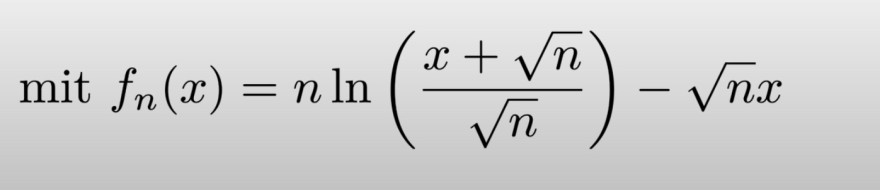
Text erkannt:
\( \operatorname{mit} f_{n}(x)=n \ln \left(\frac{x+\sqrt{n}}{\sqrt{n}}\right)-\sqrt{n} x \)
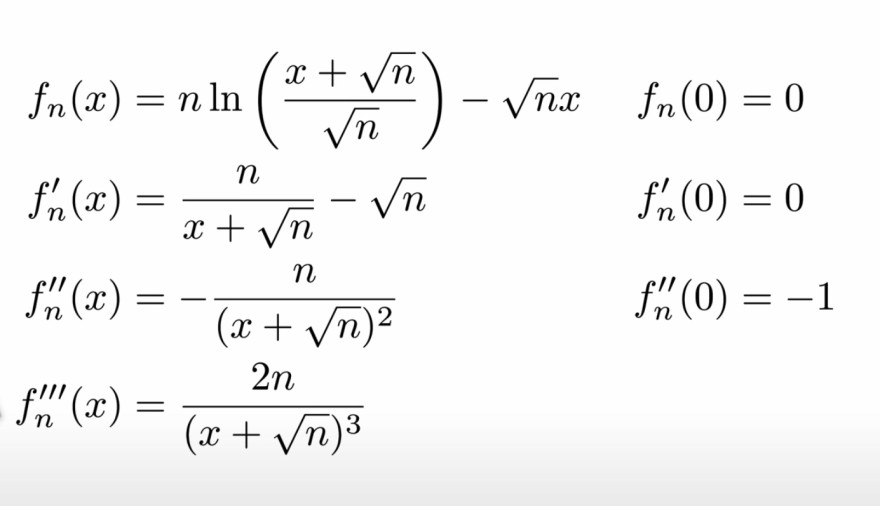
Text erkannt:
\( \begin{aligned} f_{n}(x) & =n \ln \left(\frac{x+\sqrt{n}}{\sqrt{n}}\right)-\sqrt{n} x & f_{n}(0)=0 \\ f_{n}^{\prime}(x) & =\frac{n}{x+\sqrt{n}}-\sqrt{n} & f_{n}^{\prime}(0)=0 \\ f_{n}^{\prime \prime}(x) & =-\frac{n}{(x+\sqrt{n})^{2}} & f_{n}^{\prime \prime}(0)=-1 \\ f_{n}^{\prime \prime \prime}(x) & =\frac{2 n}{(x+\sqrt{n})^{3}} & \end{aligned} \)

Text erkannt:
Satz von Taylor.
Für jedes \( x \in \mathbb{R} \) gilt mit \( n>x^{2} \)
\( f_{n}(x)=\underbrace{f_{n}(0)+f_{n}^{\prime}(0) x+\frac{1}{2} f_{n}^{\prime \prime}(0) x^{2}}_{\text {Taylor-Polynom }}+\underbrace{\frac{1}{6} f_{n}^{\prime \prime \prime}(\xi) x^{3}}_{\text {Rest }} \)
für ein \( \xi \) zwischen 0 und \( x \).