Erzeugende Elemente Beweis

Question

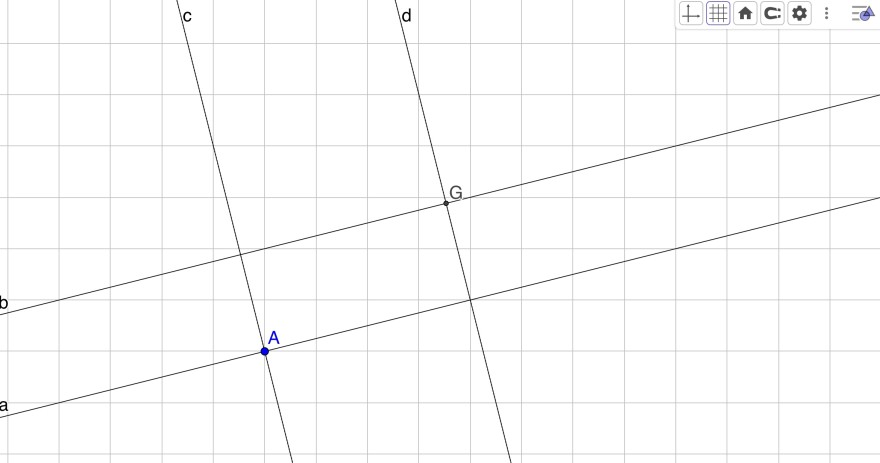
Aufgabe:

In dieser Aufgabe sollen Sie den Beweis von Satz: „Ist f:R^2→R^2

eine Kongruenzabbildung, dann ist f eine Verknüpfung von höchstens drei Achsenspiegelungen“ nacharbeiten. D.h. maximal drei Achsenspiegelungen finden, sodass sich die Verknüpfung sd∘sc∘sb∘sa
auf eine Verknüpfung dieser Achsenspiegelungen verkürzt. Sie starten daher mit drei möglichst geschickt gewählten Punkten. Dabei heißt geschickt gewählt, dass der anschließende Aufwand minimiert wird. Funktionieren wird es mit drei beliebigen nicht kollinearen Punkten.
Angegeben werden sollen jeweils Konstruktionsbeschreibungen der neuen Geraden und natürlich der Grund, warum diese konstruiert werden.

Es gibt 2 Teilaufgaben:

1.

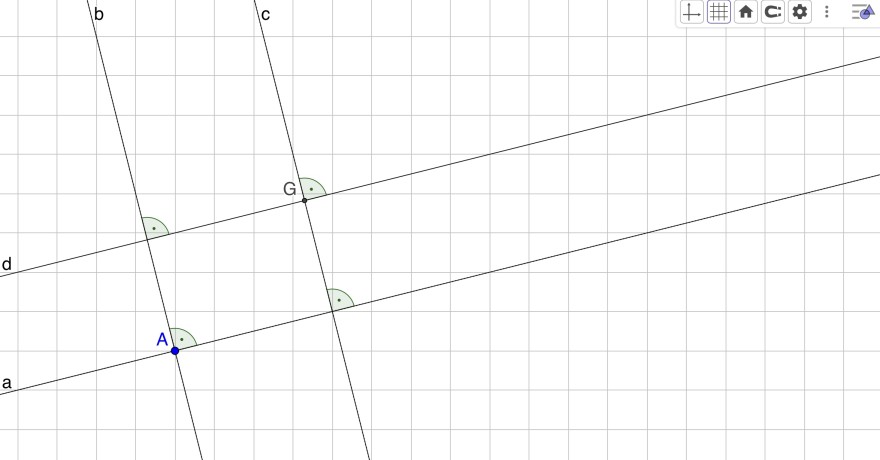
2.

Answer 1

Kongruenzabbildungen der Ebene sind Spiegelungen, Translationen und Drehungen und deren Verknüpfungen. Eine Drehung oder eine Translation ist ein Produkt von zwei Spiegelungen, ein Produkt einer Translation und eine Drehung kann also als Produkt von drei Spiegelungen dargestellt werden, da man bei einer Drehung eine Spiegelachse frei wählen kann.

Comments

Hubert Grassmann Mitglied seit 3 Monaten

genießt also noch so etwas wie Welpenschutz.