die fehlenden Werte habe ich gefunden. Hier das Modell wie in der Aufgabe, 1 cm im Modell sind 10 m in Wirklichkeit.
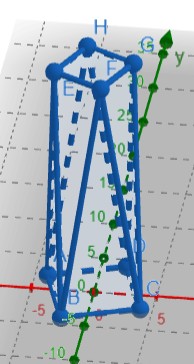
Alle Werte jetzt in cm.
B=(-2|-4|0) ; C=(4|-2|0) .
Die Strecke BC berägt also \( \sqrt{(4-(-2))^2+((-2)-(-4))^2}=\sqrt{40} \).
Du hast ein gleichschenkliges Dreieck mit der Grundline \( \sqrt{40} \) und der Höhe 42. Das sind die vier Dreiecke mit der Grundlinie unten.
Von oben sieht das so aus:
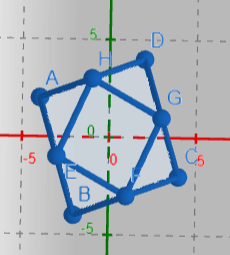
Die Strecke EF beträgt \( \sqrt{20} \). Auch hier hast du wieder eine bzw. 4 Dreiecke mit der Grundline \( \sqrt{20} \). Die Höhe ist aber mehr als 42, da das Dreieck schräg im Raum steht.
Hilft das weiter?