Zwei Kreise schneiden sich Gesamtflächeninhalt ausrechnen

Question

Zwei Kreise haben die Radien r1= 5 cm und r2= 10 cm. Der Abstand ihrer MIttelpunkte beträgt d=8 cm.

Wie groß ist die gemeinsame Fläche beider Kreise? (Erst zeichnen dann rechnen)

Wäre sehr dankbar über eine leichte Antwort vielleicht sogar mit Zeichnung :)

Comments

Ich hab da leider im Moment keine Zeit für die Rechnung. 

Hier mal, was ich in deiner Skizze ergänzen würde. Das grüne Dreieck ist nicht rechtwinklig. Die zweite Tangente sollte die Diagonale auch irgendwo schneiden. Dort kommen dann auch wieder schon vorhandene Winkel nochmals vor (wie blau). 

Nun müsste man wohl irgendwie das x berechnen, falls man keinen Winkel im grünen Dreieck findet.

Answer 1

Gesamtfläche:=Fläche des Kreises mit dem r=10cm  +  die halbe Fläche des Kreises r=5cm -  eines Kreisabschniites des Kreise r=10cm.

Durch den Radius des Großes Kreises und den Durchmesser de kleines Kreises wird ein gleichseitiges Dreieck aufgespannt, jeder winkel ist 60°

Fläche des Abschnittes = 10²/2(π*60°/180° -sin 60°)=9,0586cm

Gesamtfläche= π*10²+0,5 *5²-9,0586=317,600cm²

siehe Skizze( nicht maßstabsgetreu)

Comments

Sorry, aber ich glaube das stimmt nicht. Du gehst von einem gleichseitigen Dreieck aus. Wenn das der Fall ist, dann beträgt der Abstand der Mittelpunkte von einander 5*sqrt(3) und nicht 8, so wie gefordert...

Answer 2

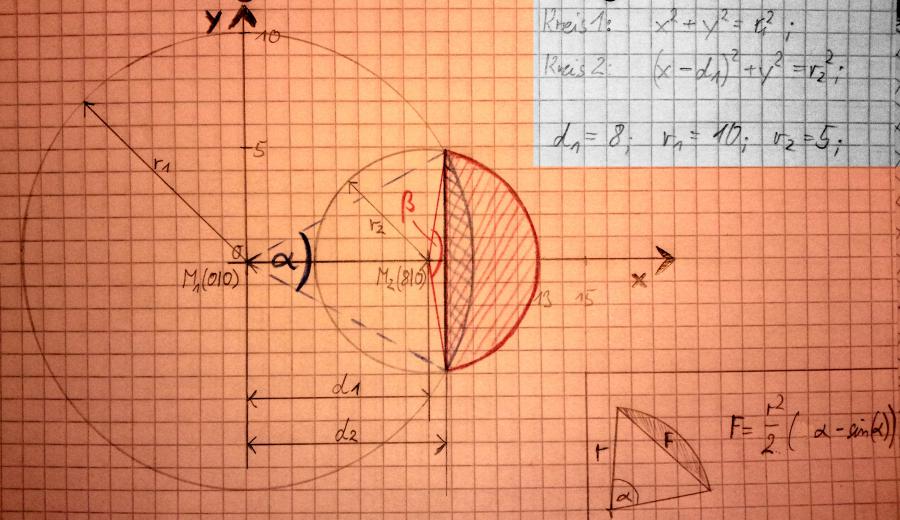
Bestimmen der x-Koordinate der Schnittpunkte: Kreisgleichung 1 minus Kreisgleichung 2

x^2 - (x -d)^2 = r1^2 -r2^2;

x = 139/16 = d2;

 

Bestimmen der Winkel:

alpha = 2*arccos(d2 / r1) ≈ 1,03625;

beta = 2*arccos( (d2 -d1) / r2) ≈ 3,00398;

 

Bestimmen der Flächen:

blaue Fläche:

Fb = r1^2 / 2 * (alpha -sin(alpha) ) =

  = r1^2 / 2 * [ 2*arccos(d2 / r1) -sin( 2*arccos(d2 / r1) ) ] =

  ≈ 8,7874 cm^2;

rote Fläche:

Fr = r2^2 / 2 * (beta -sin(beta) ) =

  = r2^2 / 2 * [ 2*arccos( (d2 -d1) / r2)  -sin( 2*arccos( (d2 -d1) / r2) ) ] =

  ≈ 35,835 cm^2;

 

Bestimmen der gemeinsamen Fläche: (Hier bin ich mir nicht ganz sicher ob Du die Schnittmenge meinst oder die Vereinigungsmenge)

Hier mal die Rechnung für die Schnittfläche:

F2 = r2^2 *pi = 78,5398 cm^2; //Fläche des kleinen Kreises mit r2;

Fs = F2 - (Fr -Fb) =

  ≈ 51,5 cm^2;

 

lg JR

Answer 3

\(c: x^2+y^2=25\)  →  \(y= \sqrt{25-x^2}\)   nur \(y≥0\)

gemeinsame Sehne liegt auf \(x=-0,69\)

Der rote Kreis hat bei \(x=5\) eine Nullstelle.

\(\red{A}=2 \cdot \int\limits_{-0,69}^{5}\sqrt{25-x^2}dx≈46cm^{2}\)

Der blaue Kreis hat bei \(x=-2\) eine Nullstelle.

\(\blue{A}=2 \cdot \int\limits_{-2}^{-0,69}\sqrt{100-(x-8)^2}dx≈ 5,2   cm^{2}\)

Zusammen sind das \(≈51,2 cm^{2}\)