Wie komme ich an die restlichen Werte heran, ohne unbrauchbare Werte zu bekommen?

Question

Aufgabe:

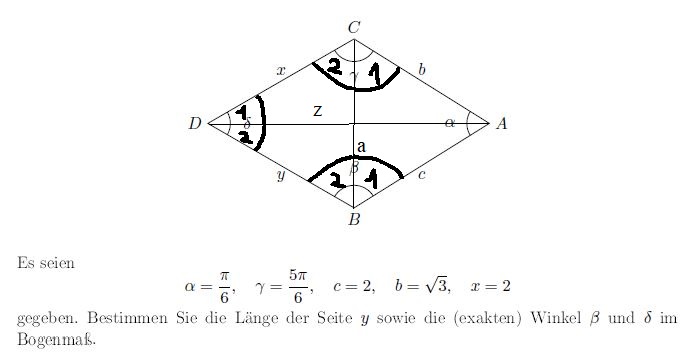
Bisher habe ich β₁ = π/3, γ₁ = π/2, γ₂ = π/3, a= 1 und z=sqrt(13)

Nun komme ich aber nicht weiter, da mir das z bisher jeden Sinussatz unbrauchbar gemacht hat. So habe ich beispielsweise für Sin(δ₁ ) = sqrt(3/13)/2

Wie komme ich an die restlichen Werte heran, ohne unbrauchbare Werte zu bekommen?

Die Aufgabe ist ohne Taschenrechner ausgelegt

Vielen Dank im Voraus!

Answer 1

Du hast im Dreieck BCD die Werte a, x, und γ2.

Drei Werte langen um das Dreieck vollständig über Sinus und Cosinussatz bestimmen zu können.

Also z.B.

y = √(a^2 + x^2 - 2·a·x·COS(γ2)) = √3

Answer 2

Wegen α + γ = π ist x || c. Das Viereck ACDB ist also ein Trapez.

Weil auch noch c = x gilt, ist das Viereck ACDB sogar ein Parallelogramm.

Comments

Angesichts der gezeigten Figur könnte man sogar vermuten, dass es sich um einen Rhombus handele. Das kann aber trotzdem nicht stimmen. Bei einer solchen Aufgabe würde ich eine weniger verwirrende Zeichnung erwarten.

Eine schrittweise nur aufgrund der gegebenen Stücke selber erstellte (und möglichst maßstäbliche) Zeichnung kann auch den Weg zur rechnerischen Lösung sehr klar erkennbar machen.

---

Ich hatte schon immer Probleme damit, mich darauf zu verlassen was ich aus Zeichnungen ablese. Mich stört es deshalb nicht, dass das Parallelogramm wie ein Rhombus aussieht obwohl es kein Rhombus ist.

---

Eine schrittweise nur aufgrund der gegebenen Stücke selber erstellte (und möglichst maßstäbliche) Zeichnung kann auch den Weg zur rechnerischen Lösung sehr klar erkennbar machen.

wie wahr - wie wahr!

Da \(\alpha + \gamma = \pi\), ist es ein Trapez und da zusätzlich \(c=x\), ist es auch ein Parallelogramm. D.h. gegenüberliegende Seiten und Winkel sind gleich lang bzw. gleich groß.

Das Dreieck \(\triangle BAB'\) ist ein gleichseitiges und \(C\) halbiert \(BB'\). Ohne Sinussatz und ohne Rechnen - nur rudimentäre Geometrie.

---

Aus welchem Grund werde ich von dir Markiert?

Meine Frage wurde am 26.05, also zwei tage vorher, gepostet und hat einen anderen Inhalt?

---

Meine Frage wurde am 26.05, also zwei tage vorher, gepostet ...

Oh - das hatte ich übersehen! Aber ich glaub' die Frage hatten wir schon zum dritten Mal ...