Aufgabe:
Ein quaderförmiges Schwimmbecken mit 11 \( m \) Länge, 7 m Breite und 4 m Höhe wird über 9 Stunden mit Wasser gefüllt.
Zu Beginn beträgt der Wasserstand \( 0.5 \mathrm{m} \) Die Änderungsrate der Wassermenge (in \( m^{3} \) pro Stunde) ist durch folgende Funktion gegeben:
$$ a(t)=0.05 \cdot t^{3}+0.4 \cdot t^{2}+2 \cdot t $$
Wie viel Wasser (in \( m^{3} \) ) befindet sich nach 7 Stunden im Becken?
a. 163.25
b. 161.21
c. 89.25
d. 124.75
e. 125.99
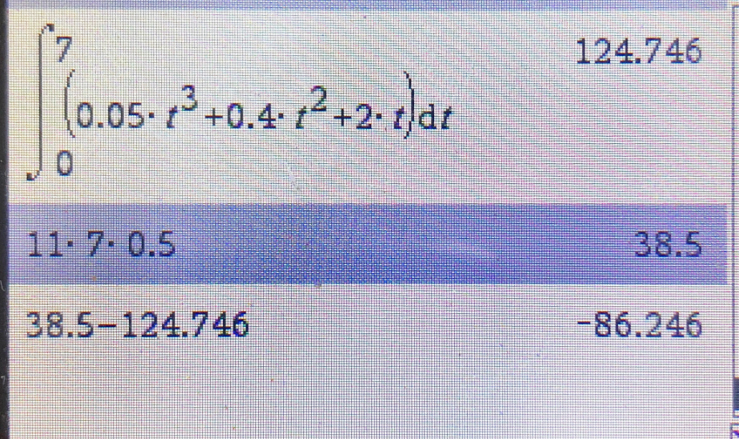
Wo liegt der Fehler?