Aufgabe:
Die Zerfallszeit von Polonium sei eine exponentialverteilte Zufallsvariable. Die Halbwertszeit dieses Elementes, d.h. die Zeit, bis zu der mit einer Wahrscheinlichkeit von 0.5 das Element zerfallen ist, beträgt 140 (Tage). Bestimmen Sie den Parameter \( \lambda \) der Exponentialverteilung.
Problem/Ansatz:
Wie geht man hier vor? Wäre E[X] = 1/lambda ein Ansatz?
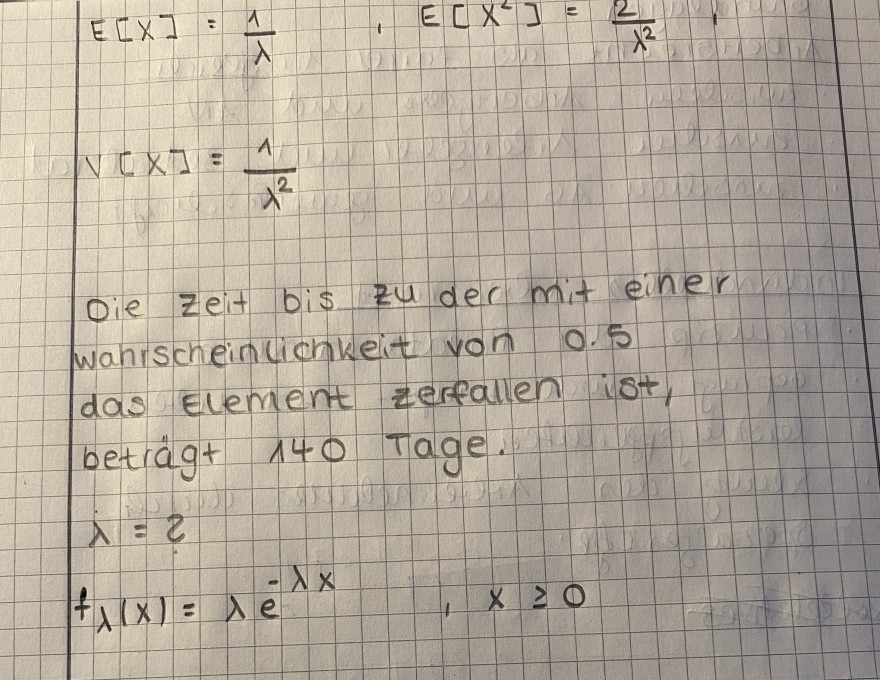
Text erkannt:
\( \begin{array}{l} E[X]=\frac{1}{\lambda} \\ V[X]=\frac{1}{\lambda^{2}} \end{array} \)
oie zeit bis zu der mit einer wahrscheincionkeit von 0.5 das Element zerfallen ist, beträgt 140 Tage.
\( \begin{array}{l} \lambda=2 \\ f_{\lambda}(x)=\lambda e^{-\lambda x} \quad, x \geq 0 \end{array} \)