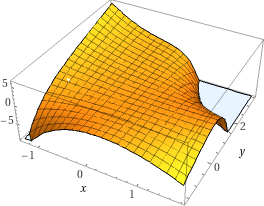
Genau. Du suchst Extrempunkte einmal auf dem Kreisrand und dann noch generell innerhalb des Kreises. Dazu benötigst du zunächst die kritischen Stellen.
f(x, y) = x^2·y - e^(x·y)
f'(x, y) = [2·x·y - y·e^(x·y), x^2 - x·e^(x·y)]
2·x·y - y·e^(x·y) = y·(2·x - e^(x·y)) = 0
x^2 - x·e^(x·y) = x·(x - e^(x·y)) = 0
Kritische Stellen wären hier (0, 0) und (1, 0).