Diff'barkeit einer Funktion mit exp zeigen -> bei mir divergiert Limes

Question

Aufgabe:

Sei \( \varphi: \mathbb{R} \rightarrow \mathbb{R} \) gegeben durch
\( \varphi(x):=\left\{\begin{array}{ll} \frac{1}{C} \exp \left(\frac{-1}{1-x^{2}}\right), & \text { falls } x \in]-1,1[, \\ 0 & \text { sonst, } \end{array}\right. \)
wobei \( C:=\int \limits_{-1}^{+1} \exp \left(\frac{-1}{1-t^{2}}\right) d t \).

Zu zeigen ist dann die stetige Diff'barkeit.

Problem/Ansatz:

Ich habe die Diff'barkeit in den Punkten \(x\in ]-1,1[\) durch einfaches berechnen der partiellen Ableitung (ist ja gleich dem totalen Differenzial ind iesem Fall) gezeigt.

Ich bin nun dabei zu zeigen, dass die Funktion auch in den Punkten \(x(-\infty,-1)\) diff'bar ist, aber da komme ich nicht weiter und erhalte tatsächlich eine Divergenz:

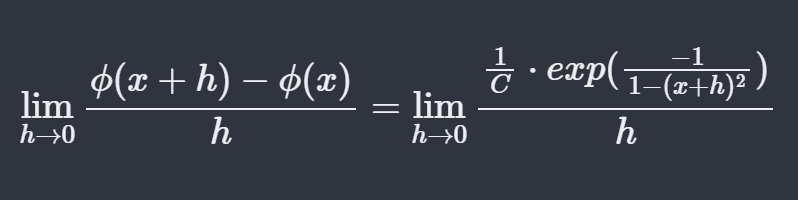
Text erkannt:

\( \lim \limits_{h \rightarrow 0} \frac{\phi(x+h)-\phi(x)}{h}=\lim \limits_{h \rightarrow 0} \frac{\frac{1}{C} \cdot \exp \left(\frac{-1}{1-(x+h)^{2}}\right)}{h} \)

wobei eben die Divergenz auftritt, wenn h eben negativ ist, da ja dann x (z.B. x=-10) plus h betraglich größer 1 sind (da ja negativ plus negativ) und dann der Ausdruck innerhalb von exp gegen einen endlichen Wert ungleich Null und ungleich 1 konvergiert, der Nenner ja aber gegen Null, was ja zur Divergenz führt.

Hab ich etwas falsch gemacht und/oder habt ihr einen besseren Ansatz?

Answer 1

Für \(x\in (-\infty;-1]\) gilt \(\varphi(x)=0\).

Comments

Ja, deswegen habe ich ja auch das \(\phi(x)\) in dem Zähler des Limes weggelassen, nur es kann ja sein, dass \(h+x\) innerhalb von \(-1,1)\) liegt, so dass dann der andere Ausdruck verwendet werden muss, oder nicht?

---

Du musst unterscheiden, ob x<-1 od x=-1 (analog auf der anderen Seite). Wenn x<-1, dann gilt auch x+h<-1 für hinreichend kleine |h| (beachte, es geht um h gegen 0).

Wenn Du Diffbarkeit im Punkt x=-1 überprüfst musst Du allerdings (auch) mit Darstellung für x>-1 arbeiten.

---

Das passt dann aber nicht zu deinem angegebenem Beispiel mit \(x=-10\) und \(h\) negativ, denn dann hättest du einen Ausdruck der Form \(\frac{0}{h}\to 0\) für \(h\to 0\). Interessant ist also nur die Differenzierbarkeit im Punkt \(x=-1\). Setze daher \(x=-1\) direkt ein.

---

Danke, das war auch mein Ansatz!

Allerdings ist dann x=-1 das Problem, denn:

\(\lim_{h\to0} \frac{\frac{1}{C}exp(\frac{-1}{1-(-1+h)^2})}{h}\) geht für h<0 leider gegen unendlich, denn \(\frac{-1}{1-(-1+h)^2}\) bleibt konstant, da ja -1 plus etwas negatives kleiner -1 wird, so dass dies quadriert auch wieder größer 1 ist. Es folgt also, dass dieser Ausdruck gegen plus unendlich läuft, aber exp(\(\infty\)) ist auch unendlich, so dass der Limes nicht existieren würde.

Oder irre ich mich?

---

Du hast dort ja immer noch nicht \(x=-1\) eingesetzt. Und im Zähler der Exponentialfunktion steht eine -1. Das würde also eher gegen \(\exp(-\infty)\) gehen...

---

Das passt dann aber nicht

Aber es gilt doch: \(\lim_{h\to0} exp(\frac{-1}{1-(-10+h)^2})=exp(\frac{-1}{1-(-10)^2})\), da ja exp stetig ist. Das bleibt dann doch aber ein endlicher Wert? Wodurch dann ein endlicher Wert durch h, wobei h->0, somit also das ganze gegen unendlich konvergiert. Oder sehe ich das falsch?

Das würde also eher gegen \(\exp(-\infty)\) gehen...

Nein, es gilt doch, dass h<0 ist. Somit ist \(\lim_{h\to0} exp(\frac{-1}{1-(h-1)^2})\) doch ein endlicher Wert, je nach gewähltem x? Da ja im Nenner gilt: \(1-(h-1)^2<0\).

---

\(\varphi(-10+h)=0\) für \(h \to 0\).

Ich hab das \(h<0\) übersehen. Aber der Fall ist doch trivial, denn \(x+h\) mit \(x\in(-\infty;1]\) und \(h<0\) liefert ebenfalls \(\varphi(x+h)=0\)!

---

Ja, das stimmt, sorry. Das hatte ich nicht bedacht, dass dann ja die ganze Funktion per definitionem Null ist. Nur dann bleibt noch das Problem mit x=-1...

---

Für \(x=-1\) geht der Zähler gegen \(\exp(-\infty)\). Dann hast du den Fall \(\frac{0}{0}\) und kannst zum Beispiel L'Hospital bemühen.

---

Ich hatte das so gedacht, da ja h negativ und/oder positiv sein kann:

---

Nochmal: Für \(h<0\) gilt \(\varphi(-1+h)=0\) Arbeite doch einfachmal mal mit der Definition der Funktion. Für diesen Fall ist offensichtlich, dass der Grenzwert 0 ist.

---

Stimmt...

Das hatte ich wieder vergessen. Danke für deine Hilfe und Ausdauer!