Rechenschritte genau erkennen

Question

Könnte mir jemand sagen was beim vorletzten Rechenschritt genau gemacht wird, sodass die Summe beim letzten Rechenschritt verschwindet? Hat es womöglich etwas mit der Produktregel zu tun?

Text erkannt:

\( \begin{array}{l} =\underbrace{\int \ldots \int}_{n \text {-mal }} \hat{\theta}\left(x_{1} \ldots, x_{n}\right)\left(\sum \limits_{i=1}^{n} \frac{d}{d \theta} \log f\left(x_{i} \mid \theta_{0}\right)\right) \prod \limits_{j=1}^{n} f\left(x_{j} \mid \theta_{0}\right) d x_{1}, \ldots, d x_{n} \\ =\int \ldots \int \hat{\theta}\left(x_{1} \ldots, x_{n}\right)\left(\sum \limits_{i=1}^{n} \frac{\frac{d}{d \theta} f\left(x_{i} \mid \theta_{0}\right)}{f\left(x_{i} \mid \theta_{0}\right)}\right) \prod \limits_{j=1}^{n} f\left(x_{j} \mid \theta_{0}\right) d x_{1}, \ldots, d x_{n} \\ =\int \ldots \int \hat{\theta}\left(x_{1} \ldots, x_{n}\right)\left(\sum \limits_{i=1}^{n} \frac{d}{d \theta} f\left(x_{i} \mid \theta_{0}\right)\right) \prod \limits_{j=1, i \neq i}^{n} f\left(x_{j} \mid \theta_{0}\right) d x_{1}, \ldots, d x_{n} \\ =\left.\int \ldots \int \hat{\theta}\left(x_{1} \ldots, x_{n}\right) \frac{d}{d \theta}\right|_{\theta=\theta_{0}} \prod \limits_{j=1}^{n} f\left(x_{j} \mid \theta_{0}\right) d x_{1}, \ldots, d x_{n} \end{array} \)

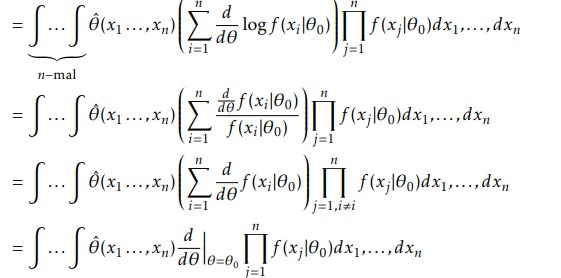
Text erkannt:

\( \begin{array}{l} =\underbrace{\int \ldots \int}_{n \text {-mal }} \hat{\theta}\left(x_{1} \ldots, x_{n}\right)\left(\sum \limits_{i=1}^{n} \frac{d}{d \theta} \log f\left(x_{i} \mid \theta_{0}\right)\right) \prod \limits_{j=1}^{n} f\left(x_{j} \mid \theta_{0}\right) d x_{1}, \ldots, d x_{n} \\ =\int \ldots \int \hat{\theta}\left(x_{1} \ldots, x_{n}\right)\left(\sum \limits_{i=1}^{n} \frac{\frac{d}{d \theta} f\left(x_{i} \mid \theta_{0}\right)}{f\left(x_{i} \mid \theta_{0}\right)}\right) \prod \limits_{j=1}^{n} f\left(x_{j} \mid \theta_{0}\right) d x_{1}, \ldots, d x_{n} \\ =\int \ldots \int \hat{\theta}\left(x_{1} \ldots, x_{n}\right)\left(\sum \limits_{i=1}^{n} \frac{d}{d \theta} f\left(x_{i} \mid \theta_{0}\right)\right) \prod \limits_{j=1, i \neq i}^{n} f\left(x_{j} \mid \theta_{0}\right) d x_{1}, \ldots, d x_{n} \\ =\left.\int \ldots \int \hat{\theta}\left(x_{1} \ldots, x_{n}\right) \frac{d}{d \theta}\right|_{\theta=\theta_{0}} \prod \limits_{j=1}^{n} f\left(x_{j} \mid \theta_{0}\right) d x_{1}, \ldots, d x_{n} \end{array} \)

Comments

Das ist echt sehr durcheinander!?

Answer 1

Du hast schon den richtigen Riecher. Hier wird die Produktregel der Differentiation angewendet und ein kleiner Rechentrick.

Bei solchen Rechnungen kann es günstig sein, auch mal die Rückwärtsrichtung durchzurechnen. In der Rechnung sind auch Schreibfehler, die ich gleich anpasse.

Um Schreibarbeit zu sparen, schreibe ich \(\partial_\theta\) statt \(\frac d{d\theta}\) und \(f_i(\theta)\) anstelle von \(f(x_i\, | \, \theta)\):

$$\left.\partial_\theta\right|_{\theta=\theta_0} \prod_{j=1}^nf_j({\color{blue}\theta})\stackrel{Produktregel}{=} \sum_{i=1}^n (\partial_\theta f_{\color{blue}i})(\theta_0) \prod_{\stackrel{j=1}{j\neq{\color{blue} i}}}^nf_j(\theta_0) \quad (1)$$

Jetzt wird im \(i\)-te Summanden der Faktor \(\frac {f_i(\theta_0)}{f_i(\theta_0)}\) eingefügt, damit man wieder das gesamte Produkt \(\displaystyle \prod_{j=1}^nf_j(\theta_0) \) hat:

$$(1) = \sum_{i=1}^n \frac{(\partial_\theta f_{\color{blue}i})(\theta_0)}{f_i(\theta_0)} \prod_{{{\color{blue} j=1}}}^nf_j(\theta_0)$$

Nun kann das Produkt der \(f_j\) ausgeklammert werden.