Gemeinsamer Punkt der Funktionsschar: ft(x) = x^2 + tx + t

Question

Ich habe die Funktion f_t(x) = x² + tx + t                    t∈ℝ

Gesucht ist der Punkt, durch den alle Schaubilder von K_t gehen.

Ich würde für t 2 Werte einsetzten einmal 2 und -0,5

und dann beide Funktionsterme gleichsetzen, den Wert den ich für x rausbekomme in den 1. oder 2. Funktionsterm einsetzten. Würde das gehen oder muss ich ertmal t bestimmen?

Comments

Eine superausführliche Erklärung die der Mathecaoch da liefert , es ist schön dass es so etwas gibt !!!!!!!!!!!!!!!!!

Answer 1

f_t(x) = x^2 + tx + t
f_s(x) = x^2 + sx + s

f_t(x) = f_s(x)
x^2 + tx + t = x^2 + sx + s
tx + t = sx + s
tx - sx = s - t
x(t - s) = s - t
x = (s - t)/(t - s) = -1

f_t(-1) = (-1)^2 + t(-1) + t = 1

Der Punkt lautet P(-1 | 1)

Hier noch eine Skizze:

 

Comments

Danke erstmal, in dieser Aufgabe geht des schon aber was ist wenn es lautet:

Zeigen Sie: Alle Parabeln K_t berühren sich in einem Punkt. Bestimmen sie ihn.

f_t(x) = tx² + (1-2t)x + t + 1     ; t∈ℝ*

da kann ich des aber nicht wie oben machen, da die Gleichung zu lang ist ich bekommen keinen normalen Wert raus und die Fragestellung ist anders.

---

Berühren bedeutet ja sie haben ein Punkt gemeinsam und in diesem Punkt ist die Steigung gleich

ft(x) = t·x^2 + (1 - 2·t)·x + t + 1
ft'(x) = 2·t·x - 2·t + 1

Nun setzte ich die Ableitungen gleich

ft'(x) = fs'(x)
2·t·x - 2·t + 1 = 2·s·x - 2·s + 1

Als Lösung bekomme ich: 

x = 1 ∨ s = t

Also ich würde hier jetzt x = 1 als Berührstelle denken. Weiß allerdings noch nicht ob sie den Punkt auch gemeinsam haben. Daher setzte ich es in die Funktionsgleichung ein

ft(1) = t·1^2 + (1 - 2·t)·1 + t + 1 = 2

Damit ist es unabhängig von t und damit ein Berührpunkt.

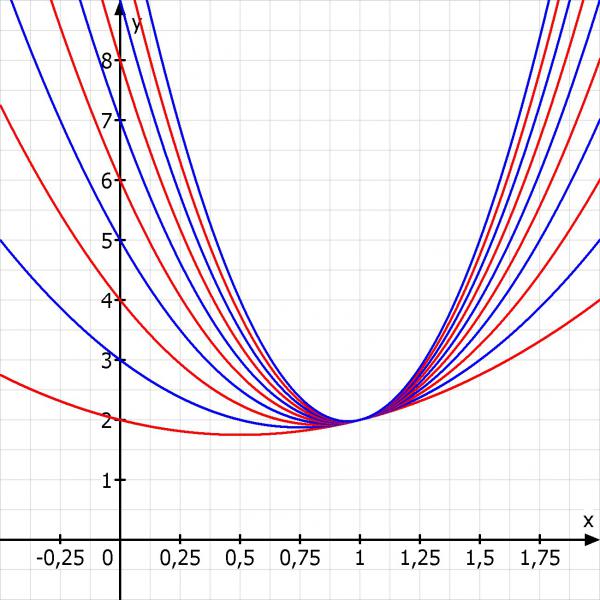
Hier noch eine Skizze:

---

Wie kommst du jetzt auf die -1 bei  " x = (s - t)/(t - s) = -1 "

---

x(t - s) = s - t 

Beide Seiten durch (t - s) teilen

x = (s - t )/(t - s)

im Zähler ein Minus ausklammern

x = -(t - s)/(t - s)

Durch (t - s) kürzen

x = -1