Aufgabe: Nr.2 c)
Verstehe nicht was genau hier richtig ist. Was ist das Ergebnis
Problem/Ansatz:
Mein Ansatz scheint mir nicht richtig 
Text erkannt:
2. Aufgabe
(19 Punkte)
Es sei \( f: \mathbb{R}^{2} \rightarrow \mathbb{R} \) gegeben durch
\( f(x, y)=\arctan (x y) \)
(a) Bestimmen Sie alle ersten und zweiten partiellen Ableitungen von \( f \).
(b) Bestimmen Sie die kritischen Punkte von \( f \) und geben Sie jeweils an, ob es sich um Maximalstellen, Minimalstellen oder Sattelpunkte handelt.
(c) Geben Sie das Taylorpolynom \( T_{1} f(x) \) erster Ordnung von \( f \) um die Entwicklungsstelle \( \left(x_{0}, y_{0}\right)=(1,1) \) an. Hinweis: Es gilt \( \tan (\pi / 4)=1 \).
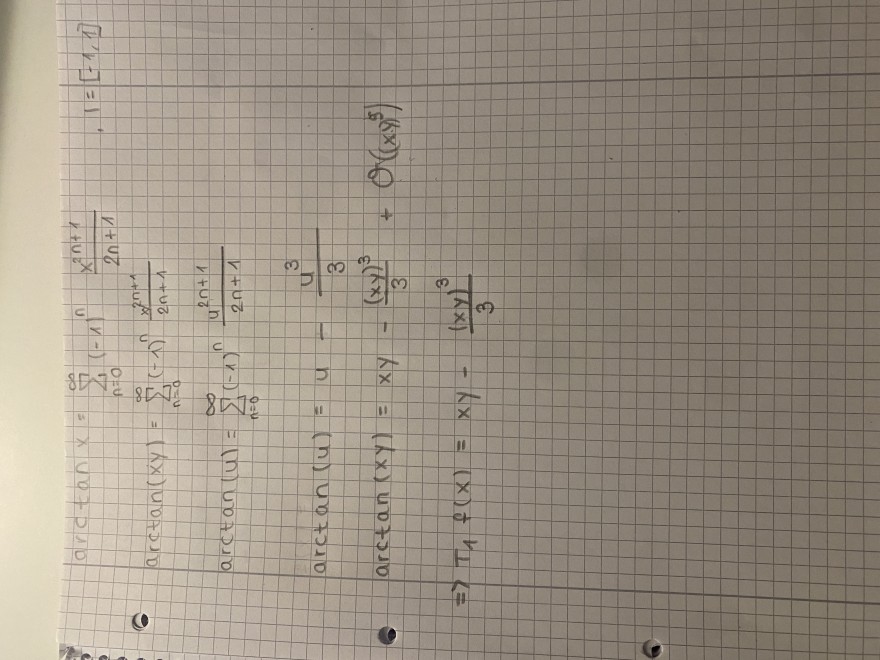
Text erkannt:
\( \begin{array}{l}\arctan x=\sum \limits_{n=0}^{\infty}(-1)^{n} \frac{x^{2 n+1}}{2 n+1} \quad, \quad=[-1,1] \\ \arctan (x y)=\sum \limits_{n=0}^{\infty}(-1)^{n} \frac{x^{2 n+1}}{2 n+1} \\ \arctan (u)=\sum \limits_{n=0}^{\infty}(-1)^{n} \frac{u^{2 n+1}}{2 n+1} \\ \arctan (u)=u-\frac{u^{3}}{3} \\ \arctan (x y)=x y-\frac{(x y)^{3}}{3}+O\left((x y)^{9}\right) \\ \Rightarrow T_{1} f(x)=x y-\frac{(x y)^{3}}{3}\end{array} \)
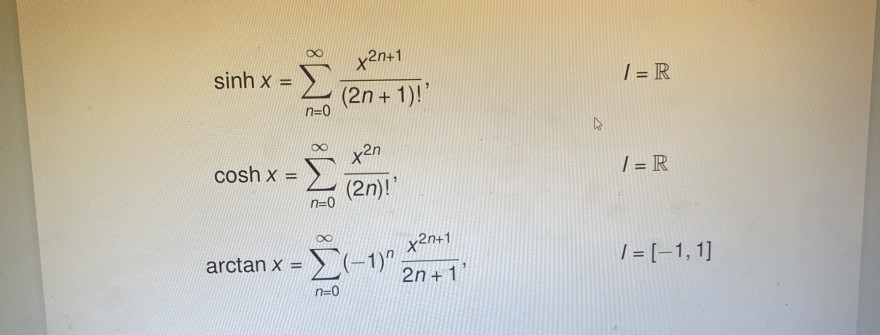
Text erkannt:
\( \begin{array}{ll}\sinh x=\sum \limits_{n=0}^{\infty} \frac{x^{2 n+1}}{(2 n+1)!}, & I=\mathbb{R} \\ \cosh x=\sum \limits_{n=0}^{\infty} \frac{x^{2 n}}{(2 n)!}, & I=\mathbb{R} \\ \arctan x=\sum \limits_{n=0}^{\infty}(-1)^{n} \frac{x^{2 n+1}}{2 n+1}, & I=[-1,1]\end{array} \)