Vom Punkt T (50|-50|100) fällt Licht in Richtung (-1-а|3-a|a-2). Zeigen Sie, dass ein Lichtstrahl von Punkt…

Question

Aufgabe: d) Vom Punkt T (50|-50|100) fällt Licht in Richtung

(-1-а|3-a|a-2). Zeigen Sie, dass ein Lichtstrahl von Punkt T auf den Punkt S fällt.

Problem/Ansatz: ich verstehe nicht, welche Rechnung gefordert wird.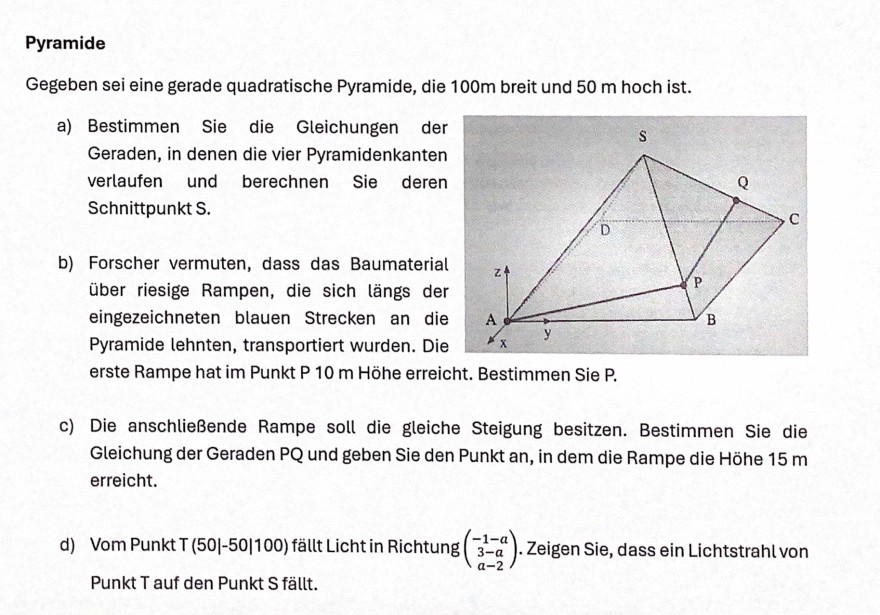

Text erkannt:

Pyramide
Gegeben sei eine gerade quadratische Pyramide, die 100 m breit und 50 m hoch ist.
a) Bestimmen Sie die Gleichungen der Geraden, in denen die vier Pyramidenkanten verlaufen und berechnen Sie deren Schnittpunkt S.
b) Forscher vermuten, dass das Baumaterial über riesige Rampen, die sich längs der eingezeichneten blauen Strecken an die Pyramide lehnten, transportiert wurden. Die erste Rampe hat im Punkt P 10 m Höhe erreicht. Bestimmen Sie P.
c) Die anschließende Rampe soll die gleiche Steigung besitzen. Bestimmen Sie die Gleichung der Geraden PQ und geben Sie den Punkt an, in dem die Rampe die Höhe 15 m erreicht.
d) Vom Punkt T (50|-50|100) fällt Licht in Richtung \( \left(\begin{array}{c}-1-a \\ 3-a \\ a-2\end{array}\right) \). Zeigen Sie, dass ein Lichtstrahl von Punkt T auf den Punkt S fällt.

Comments

Ich verweise hier nur auf die ähnliche Aufgabe

https://www.mathelounge.de/381850

Dort sollte nachgewiesen werden, dass die ganze Kante BS von Lichtstrahlen getroffen wird. Damit hat man auch gezeigt, dass speziell die Spitze S getroffen wird.

Answer 1

Der Lichtstrahl ist math. eine Gerade, diese beschreibt man am besten in Punkt-Richtungsform. Suche also die Stichworte "Punkt", "Richtung" in der Aufgabenstellung, stelle die Geradengleichung auf und prüfe, ob der Punkt S auf dieser Geraden liegt.

Dass da noch eine neue Unbekannte a auftaucht, ist kein Problem. Du wirst sehen, Du erhältst ja drei Gleichungen.

Answer 2

d)

[50, -50, 100] + r * [-1 - a, 3 - a, a - 2] = [-50, 50, 50] --> a = 1 ∧ r = 50

Punkt S wird von dem Lichtstrahl der Geraden mit a = 1 der Schar getroffen. r ist dabei 50.