Knickfrei heißt, die Steigung ändert sich nicht sprunghaft.
Eine Funktion, die an einer bestimmten Stelle knickfrei ist, kann dort auch ruckfrei sein, muss es aber nicht. Ruckfrei heißt, dass an der Stelle sowohl die y-Werte, als auch die erste Ableitung und die zweite Ableitung links und rechts von dem Punkt identisch sind.
Der Übergangsbogen ist üblicherweise eine kubische Funktion wenn knickfrei und eine Polynomfunktion ("ganzrationale Funktion*) fünften Grades wenn ruckfrei. Dann braucht es sechs Gleichungen im Steckbrief, weil sie sechs Koeffizienten hat.
Blaue Kurve knickfrei, gelbe Kurve ruckfrei:
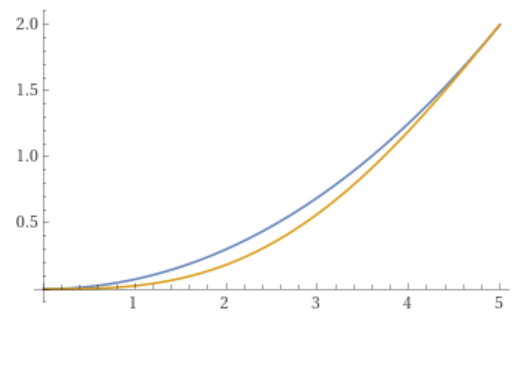
Ich würde den Unterschied so erklären, das bei der gelben Kurve an der Übergangsstellen die Fahrtrichtung nicht ruckartig von "geradeaus" auf "Kurve" bzw. umgekehrt ändert wird, sondern kontinuierlich.