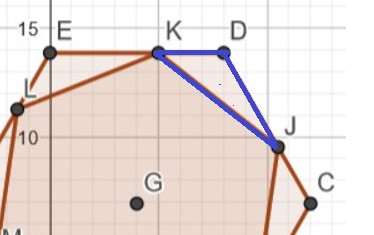
Sei KD =CJ =x.
Der Inhalt des Dreiecks KJD ist dann 0,5·sin 120° · x · (8-x), und alle 6 Dreiecke dieser Form haben zusammen den Inhalt 1,5\( \sqrt{3} \)· x · (8-x).
Das große Sechseck hat einen Inhalt von 6·(0,5·sin 60° · 8 · 8)= 96\( \sqrt{3} \), das innere Sechseck nur 49/64 davon. Die Differenz der beiden Sechseckflächen ist
\( \frac{15}{64} \) ·96\( \sqrt{3}\) = \( \frac{45}{2} \) ·\( \sqrt{3}\)
und entspricht der oben berechneten Summe der 6 kleinen Dreiecksflächen.
Es gilt also 1,5\( \sqrt{3} \)· x · (8-x)=\( \frac{45}{2} \) ·\( \sqrt{3}\).
Daraus folgt x · (8-x)=15 mit x=3 und 8-x=5 (oder x=5 und 8-x=3).
Das Teilungsverhältnis 3:5 aus der anderen Antwort wird bestätigt.