Stetigkeit problematische Aussagen

Question

Aufgabe:

Was ist an der Vorstellung problematisch: "Eine Funktion ist stetig, wenn ihr Graph keine Sprünge hat?" und "Eine Funktion ist stetig, wenn ihr Graph ohne abzusetzen durchgezeichnet werden kann?"

Comments

"Eine Funktion ist stetig, wenn ihr Graph keine Sprünge hat?" und "Eine Funktion ist stetig, wenn ihr Graph ohne abzusetzen durchgezeichnet werden kann?"

Das ist ein saloppe, unmathematische Aussage, weil nicht sauber definiert.

---

Und das ist eine nicht passende Antwort, weil es um die "Vorstellung" geht und nicht um die genaue mathematische Definition. Für viele Funktionstypen ist diese Vorstellung durchaus brauchbar, gerade wenn es darum geht, den Begriff der Stetigkeit zu veranschaulichen. Eine Funktion, deren Graph (offensichtliche) Sprünge enthält, kann nicht stetig sein.

Die Frage war, was an dieser Vorstellung problematisch ist. Ein Beispiel dafür hat nudger in seiner Antwort gegeben.

---

Ein Beispiel dafür hat nudger in seiner Antwort gegeben.

Wieso? Diese Funktion ist nicht stetig und kann nicht "ohne abzusetzen" gezeichnet werden

---

Dann betrachte ich nur rationale \(x\)-Werte. Dann könnte ich den Graphen praktisch zeichnen bzw. visualisieren, sehe aber weder Sprünge, noch die eigentlichen Löcher darin. Der Graph würde dann aber den Anschein erwecken, die Funktion wäre stetig.

---

Dann könnte ich den Graphen praktisch zeichnen

Nein, nur theoretisch.

Answer 1

Betrachte z.B. die https://de.m.wikipedia.org/wiki/Dirichlet-Funktion und versuche mal selbst den Graphen zu zeichnen.

Answer 2

Die Aussage ,,Eine Funktion ist stetig, wenn ihr Graph ohne abzusetzen durchgezeichnet werden kann‘‘ ,ist unmathematisch und falsch. So solltest du Stetigkeit nicht lernen. Stetigkeit kannst du dir am besten mit der Epsilon-Delta-Definition veranschaulichen (falls du das schon hattest).

Hier zwei Beispiele, warum die obige Aussage formal verkehrt ist.

Erstes Beispiel:

Betrachte z.B. f : |R \ {0} —> |R, f(x) := 1/x.

Die Funktion hat bei der Geraden mit x = 0 (also die y-Achse) eine Asymptote und divergiert dann für 0 > x —> 0 gegen die negative und für 0 < x —> 0 gegen die positive Unendlichkeit, wodurch sie da also einen unendlich langen Sprung hat. Du kannst also den Graph von f nicht ohne absetzen zeichnen.

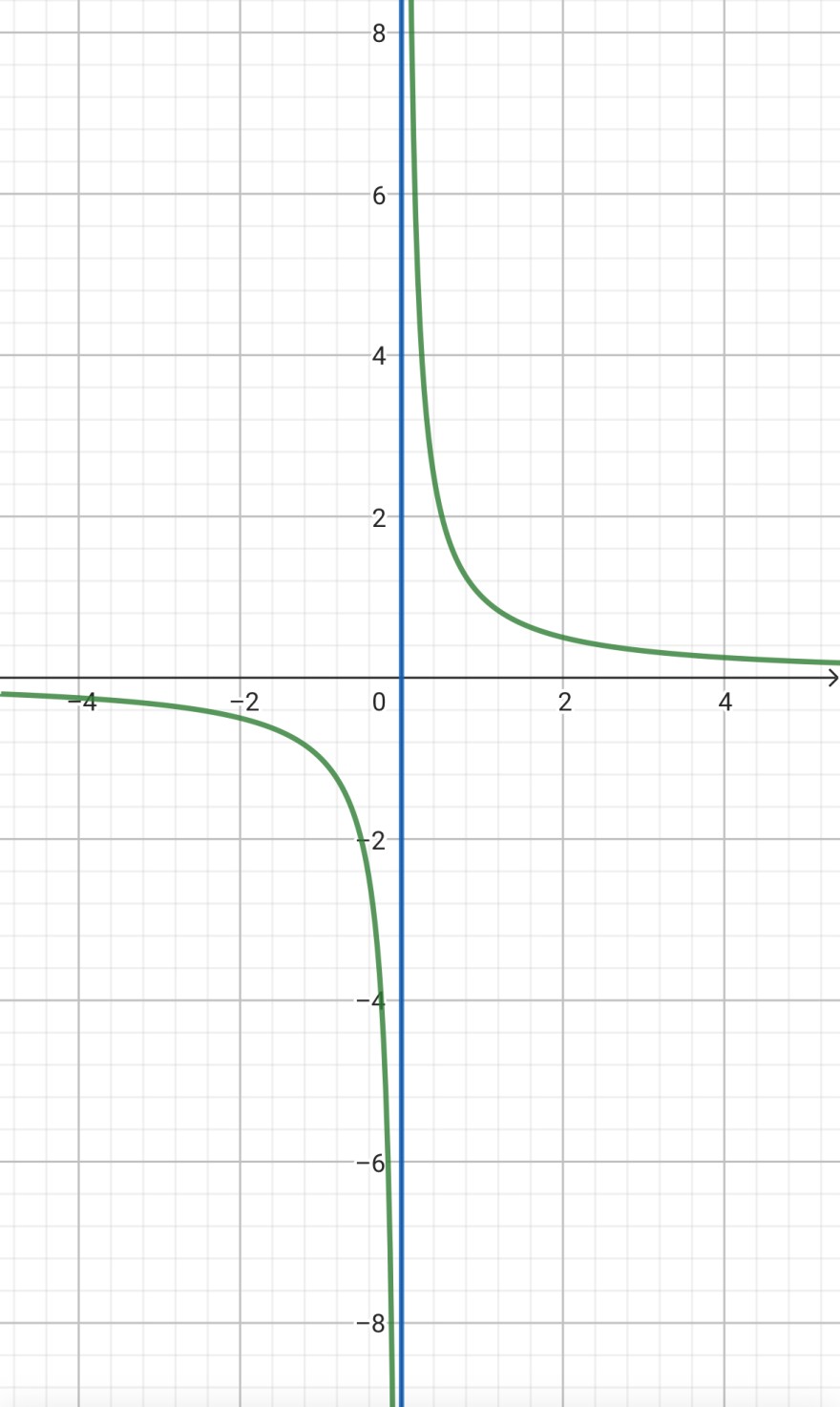
Quelle: Geogebra

Zweites Beispel: (Das Beispiel ist etwas fortgeschrittener, also widme dich eher dem ersten Beispiel, falls du soetwas nicht kennst)

Die Funktion z : |R^4 —> |R, z(x,y,z,t) := xyzt, ist ganz offensichtlich stetig, aber ist das wirklich deswegen, weil ihr Graph ohne Stopp gezeichnet werden kann?!

Hier ist G(z) = {(x,y,z,t, xyzt)^T : x,y,z,t in |R} der Graph von z im |R^5 und diese Menge kann man weder zeichnen noch sich ansatzweise irgendwie bildlich vorstellen.

Comments

Es wurde aber nicht nach der Definition von Stetigkeit gefragt, sondern warum diese Vorstellung problematisch ist. Darauf gehst du aber nicht ein.

---

Ja, mein Beispiel zeigt, warum diese Vorstellung problematisch und falsch ist.

Die Epsilon-Delta-Definition ist eine gute Methode um Stetigkeit zu veranschaulichen und zu dem auch richtig,

---

Wieso? Den Sprung sehe ich auch, wenn ich den Graphen vor mir habe. Und ich sehe auch, dass ich den Graphen nicht ohne abzusetzen zeichnen kann. Damit passen die beiden Aussagen doch wunderbar. Dafür brauche ich Epsilon-Delta nicht. Das Beispiel ist also gar nicht geeignet, um die Problematik aufzuzeigen.

---

Also ich habe Stetigkeit damals durch der Epsilon-Delta-Definition gut veranschaulichen können (dazu gibt es in Fachliteratur-Bücher auch viele Skizzen, die helfen). Ist ja nur eine Empfehlung, jeder lernt es anders.

---

Das mag ja sein. Darum geht es aber in der vom FS gestellten Frage nicht.

Versuche mal einem Schüler, der jetzt vielleicht nicht das notwendige Wissen hat, das Epsilon-Delta-Kriterium zu veranschaulichen ohne da groß auszuschweifen.

---

Seit wann macht man in der Schule das Thema Stetigkeit?

---

Es gibt durchaus noch Schulen, wo das behandelt wird, oft mit technischem Schwerpunkt.

Ich könnte mir sogar vorstellen, dass die Frage aus einem Lehramtsstudium stammt, denn man sollte als Lehrkraft natürlich wissen, dass die Vorstellung zwar sinnvoll ist, aber eben auch ihre Probleme hat.

---

Ja, also wenn der FS ein Schüler ist, dann ist das Epsilon-Delta-Kriterium natürlich erstmals keine Hilfe. Ich bin davon ausgegangen, das der FS zumindest im ersten Semester ist. Wir hatten damals Stetigkeit nicht in der Schule. Ich habe es zum ersten mal im Vorkurs an meiner Universität gehört und sogar da wurde es mit diesem Zeichen definiert.

Answer 3

Betrachte auch mal die Funktion \(f:\mathbb{R}\setminus \{0\}\to \mathbb{R},\ x\mapsto \frac{\sin(x)}{x}\).

Sie ist in \(x=0\) stetig fortsetzbar mit \(f(0)=1\). Man kann den Graphen also prinzipiell ohne abzusetzen zeichnen und der Graph hat auch keinen Sprung, allerdings ist die Funktion dort nicht stetig, da sie dort nicht definiert ist. Sie enthält quasi ein Loch, das schwierig zu visualisieren ist.

Außerdem ist die Aussage mit dem Zeichnen für Funktionen im Mehrdimensionalen problematisch, weil die Visualisierung des Graphen in Form einer Kurve so nicht mehr gegeben ist.

Comments

Man kann den Graphen also prinzipiell ohne abzusetzen zeichnen

Praktisch aber nicht, weil man an der Stelle x=0 doch den Stift heben muss.