Aufgabe:
An welchen Stellen sind die folgenden Funktionen komplex differenzierbar? Begründen Sie jeweils sowohl über die Cauchy-Riemann-Differentialgleichungen als auch über den Differenzenquotienten.
i) f(z) := z(komplex konjugiert)*z(normal) 2
ii) f(x + iy) := x 3 − 3xy 2 + i(3x 2y − y 2)
Problem/Ansatz:
Zuerst Cauchy-Riemann-Differentialgleichungen:
i) f(z)=(x−iy)(x+iy)2=(x−iy)(x2+2ixy−y 2) = x3 +xy2+ i(x2y+y3)
u(x,y)= x 3 +xy2 v(x,y)=(x2y+y 3)
∂u/ ∂x = 3x 2 +y2 ∂u/ ∂y = 2xy
∂v/ ∂x = 2xy ∂v/ ∂y= x 2 +3y 2
∂u/ ∂x =∂v/ ∂y und ∂u/ ∂y= -∂v/ ∂x
Diese Gleichungen sind im Allgemeinen nicht erfüllt, außer im Fall
x=0 und y=0 (also bei z=0). Daher sind die Cauchy-Riemann-Gleichungen nur an der Stelle z=0 erfüllt.
Stimmt das so ? Ich bin mir nicht sicher ob ich das vorgehen richtig angewandt habe.
ii) f(x + iy) := x 3 − 3xy2 + i(3x 2y − y2)
u(x,y)= x3 − 3xy2 v(x,y)= (3x 2y − y2 ) wo ich mit u/ ∂x =∂v/ ∂y und ∂u/ ∂y= -∂v/ ∂x auf das komme:
3x 2−3y2=3x 2−3y 2
−6xy=−6xy
Diese Gleichungen sind für alle x und y erfüllt und somit komplett diffbar.
Jetzt kommt das mit dem Differentialquotienten wo ich meine Probleme habe, da müsste jetzt ja das gleiche rauskommen oder ?
Bei i)
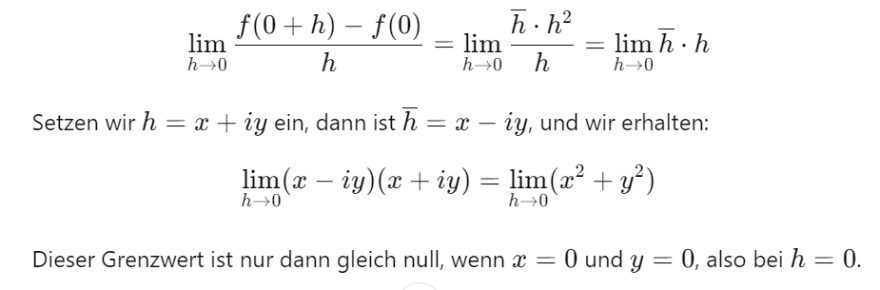
Ist das so richtig? darf ich einfach das f(0) annehmen?
wie würde das für ii) aussehen, ich hab bei ii) nämlich was anderes als beim Cauchy-Riemann-Differentialgleichungen herausbekommen kann das sein?