Wo liegt hier der Fehler…

Question

Hallo,

Folgende Aufgabe ich muss aus den 3 Bedinungsgleichungen auf die Funktion kommen

Ich habe sie komplett falsch gelöst aber vielleicht könnt ihr mir erklären warum. undzwar wollte ich erst c herausfinden und habe die 3 Gleichung mal 3 genommen um dann das Additionsverfahren zu nutzen da fällt doch dann a und B weg und c ist 13 aber warum ist das falsch ?

Wäre nett wenn ihr auf meine Frage antwortet, und nicht die Lösung gibt

Comments

Die 10 ist falsch, sie steht in der 2.

Tipp:

c= 10-2b

Setze das in 1. ein und erhalte 2 Gleichungen nur mit a und b.

---

ich muss aus den 3 Bedinungsgleichungen auf die Funktion kommen

Waren die Bestimmungsgleichungen so vorgegeben oder wie bist du auf die gekommen. Für eine Steckbriefaufgabe wären die so sehr ungewöhnlich.

9·a + 3·b + c = 3
2·b + c = 10
3·a + b = -1

Je nach Bundesland und Lehrer darf man zum Lösen linearer Gleichungssysteme noch den TR benutzen.

a = -1 ∧ b = 2 ∧ c = 6

Allerdings ist in 5 Jahren (2029) auch in Hamburg ein TR verboten, der lineare Gleichungssysteme lösen kann. Spätestens dann müssen die Schüler das nicht nur im Hilfsmittel freien Teil unter Beweis stellen, dass sie wissen, wie sowas gelöst wird.

---

In Bayern also bei uns müssen wir es ohne TR machen, wäre ich mal lieber in Hamburg...

Answer 1

Du hast dich einfach verschrieben. Da, wo Du beide Gleichungen addierst, hast Du rechts 10 stehen. Es sollte aber 3 sein.

Du hast wohl auf die falsche Zeile geschaut.

Comments

Kann man solche Aufgaben auch schneller lösen ohne diese Verfahren zu benutzen, bzw. gibt es da auch andere Möglichkeiten, ich habe in einem Video vom Gaus verfahren gehört ist das mit dem möglich?

---

ich habe in einem Video vom Gaus verfahren gehört ist das mit dem möglich?

Das ist nur eine abstraktere Form der bekannten Verfahren.

Hier kannst du das Problem lösen, indem du es auf 2 Variablen reduzierst. Siehe meinen Tipp.

---

Was würdest du allgemein empfehlen, wenn man 4 Gleichungen hat, sollte man das Gaus verfahren lernen um es schneller lösen zu können oder soll man bei den klassischen bleiben?

---

Wie gesagt: Gauß ist nur eine Abstraktion des bekannten Additions-/Substraktionsverfahrens.

https://studyflix.de/mathematik/gaus-algorithmus-2993

---

Vielleicht noch 2 Vorteile des Gauss-Verfahrens:

1. Es führt systematisch zur Lösung, man läuft nicht Gefahr, sich zu verzetteln

2. Es garantiert insbesondere auch dann die exakte Lösungsmenge, wenn die Lösung nicht eindeutig ist

Answer 2

Falls der Graph einer Funktion gegeben ist, bietet sich auch folgender Lösungsweg an:

Der Scheitel ist S\((-3|-2)\) Außerdem gibt es einen Punkt P\((2|3)\)

Hier ist die Scheitelpunktform der Parabel zielführend:   \( f(x)=a(x-x_S)^2+y_S\)

\( f(x)=a(x-(-3))^2-2=a(x+3)^2-2\)

P\((2|3)\):

\( f(2)=a(2+3)^2-2\)

\( 25a-2=3\)     \( 25a=5\)       \(a=\frac{1}{5}\)

\( f(x)=\frac{1}{5}(x+3)^2-2\)

------------------------------------------------------------

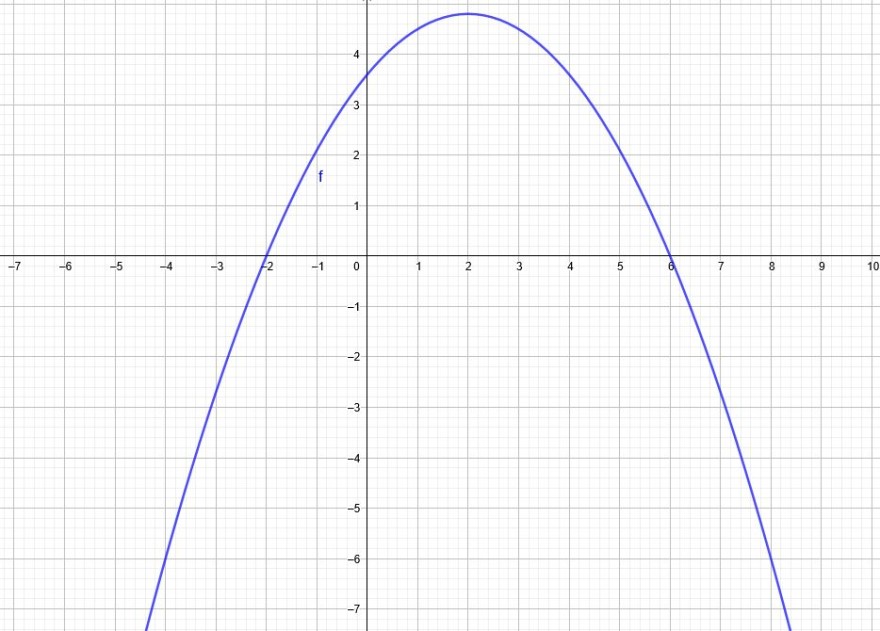
Hier ist die Nullstellenform der Parabel angebracht:     \(y=a(x-N_1)(x-N_2)\)

\(y=a[x-(-2))(x-6)]=a[(x+2)(x-6)]\)

Q\((8|-6)\):

\(y=a[(8+2)(8-6)]=20a\)

\(20a=-6\)

\(a=-\frac{3}{10}\)

\(y=-\frac{3}{10}(x+2)(x-6)\)

Answer 3

2·b + c = 10 --> c = 10 - 2·b

3·a + b = -1 → a = (- b - 1)/3

Das setzt man jetzt in die erste Gleichung ein und löst nach b auf

9·((- b - 1)/3) + 3·b + (10 - 2·b) = 3 --> b = 2

Wenn man jetzt b hat, kann man direkt mit den zuerst umgestellten Gleichungen a und c berechnen und ist fertig.

a = (- (2) - 1)/3 = -1

c = 10 - 2·(2) = 6

Die Zahlen sind so schön und einfach, dass solche Aufgabe hier in Hamburg auch so im hilfsmittelfreien Teil drankommt.