Meine Fragen: Wo liegt hier der Fehler?

Question

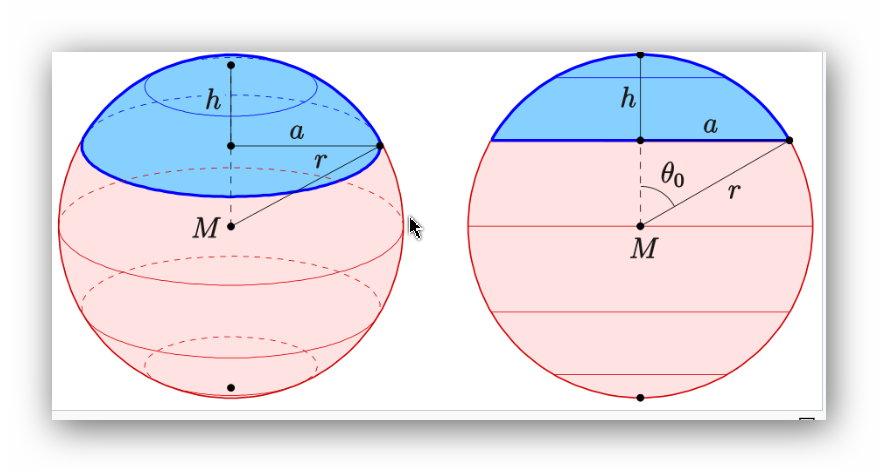
Aufgabe: Oberfläche einer Kugelhaube bestimmen

Problem/Ansatz:

Bei der Oberfläche einer Kugelkappe habe ich die folgenden Werte bereits berechnen können: h = 0,785 km; a = 629 km; θ₀ = 0,9°; r = 6370 km.

Bei vier in der Wikipedia im Artikel "Kugelsegment" angegebenen Formeln für die Oberfläche des Kugelsegments bekomme ich für die obigen Werte ein Ergebnis, das etwa bei 62.833 km² liegt; bei der fünften Formel weicht das Ergebnis um 70 km² ab.

Im Lösungsheft meines Lehrbuchs finde ich jedoch folgendes Ergebnis:
"Die Fläche der Kugelhaube lautet 2r π h = 4 π r2 sin² (a/2) = 31.453 km"

^{Das ist fast genau die Hälfte des Ergebnisses, das ich mit den Wikipedia-Formeln bekomme.
Meine Fragen: Welche der Formeln ist falsch? Oder habe ich etwas falsch verstanden?}

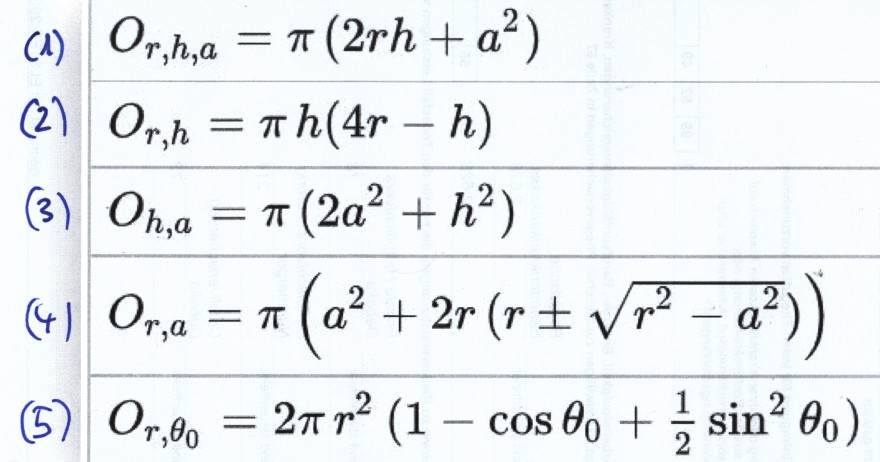
Text erkannt:

(1) \( O_{r, h, a}=\pi\left(2 r h+a^{2}\right) \)
(2) \( O_{r, h}=\pi h(4 r-h) \)
(3) \( O_{h, a}=\pi\left(2 a^{2}+h^{2}\right) \)
(4) \( O_{r, a}=\pi\left(a^{2}+2 r\left(r \pm \sqrt{r^{2}-a^{2}}\right)\right) \)
(5) \( O_{r, \theta_{0}}=2 \pi r^{2}\left(1-\cos \theta_{0}+\frac{1}{2} \sin ^{2} \theta_{0}\right) \)

Answer 1

Ich finde das ist offensichtlich

Ihr bekommt die Formel

Fläche der Kugelhaube:

A = 2·r·π·h

Bei Wikipedia steht

Oberfläche:

O = π·(2·r·h + a^2) = 2·π·r·h + π·a^2

Finde jetzt den Unterschied und sage, worin dieser wichtige Unterschied besteht.

Comments

Für mich Autodidakten ist es nicht offensichtlich, deshalb meine Anfrage auf Mathelounge. Ist mit "Fläche" und "Oberfläche" jeweils etwas anderes gemeint? Bei der Aufgabe geht es um Umfang und Fläche des "Weißwurstäquators", eines Kreises mit dem Radius von 100 km um München. Da es hier um sphärische Trigonometrie geht, denke ich, dass mit der Frage des Lehrbuchs "Welche Fläche umschließt der Weißwurstäquator?" nur die Kugelhaube gemeint sein kann, aber nicht eine ebene Fläche. Habe ich das falsch verstanden?

---

Die Oberfläche ist die Fläche, die einen Körper nach außen begrenzt. Bei einer Kugelkappe gehört dazu auch die Kreisfläche, die beim Schnitt entsteht.

Das ist wie bei einer Pyramide der Unterschied zwischen Oberfläche und Mantelfläche.

Ich hatte den Unterschied für Autodidakten extra rot gefärbt zur leichteren Erkennbarkeit.

---

Ich verstehe also nun: Die Mantelfläche M ist also um die Fläche des Schnittkreises kleiner als die Oberfläche, und nach dieser Mantelfläche ist in der Aufgabe vom Weißwurst-Äquator denn auch gefragt, während ich mich irrtümlich an die Formeln für die Oberfläche in der Wikipedia hielt. Danke für die Aufklärung!

---

Ja. Nur dass man zu einer Kugelhaube bzw. Kugelkappe nicht Mantelfläche sagt. Das ist hier einfach die Fläche der Kugelkappe oder der Kugelhaube.

Mantel sagt man z.B. bei einer Pyramide oder einem Kegel. Damit meint man dann die Oberfläche abzüglich der Grundfläche.