Für die Determinante B muss -4 rauskommen, ich habe es 2 mal berechnet aber finde meinen Rechenfehker einfach nicht, könnte mir jemand bitte behilflich sein
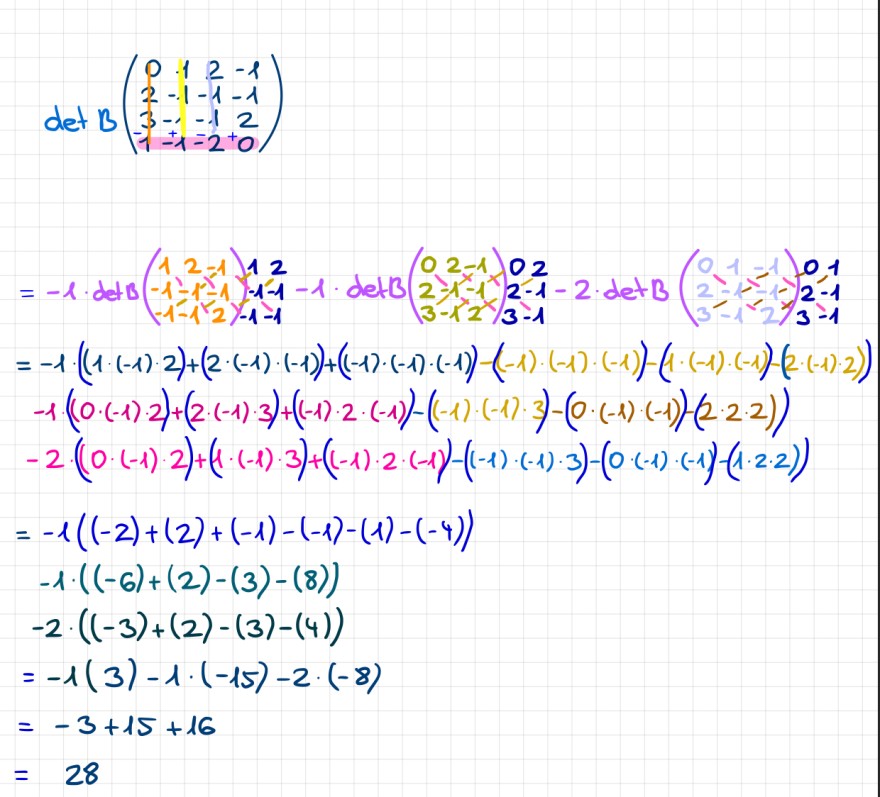
Text erkannt:
\( \operatorname{det} B\left(\begin{array}{cccc}0 & 1 & 2 & -1 \\ 2 & -1 & -1 & -1 \\ -3 & -1 & -1 & 2 \\ -1 & -1 & -2 & 0\end{array}\right) \)
\( \begin{array}{l} =-1 \cdot((1 \cdot(-1) \cdot 2)+(2 \cdot(-1) \cdot(-1))+((-1) \cdot(-1) \cdot(-1))-(-1) \cdot(-1) \cdot(-1))-(1 \cdot(-1) \cdot(-1)) \cdot(2 \cdot(-1) \cdot 2)) \\ -1 \cdot((0 \cdot(-1) \cdot 2)+(2 \cdot(-1) \cdot 3)+((-1) \cdot 2 \cdot(-1))-((-1) \cdot(-1) \cdot 3)-(0 \cdot(-1) \cdot(-1))-(2 \cdot 2 \cdot 2)) \\ -2 \cdot((0 \cdot(-1) \cdot 2)+(1 \cdot(-1) \cdot 3)+((-1) \cdot 2 \cdot(-1))-((-1) \cdot(-1) \cdot 3)-(0 \cdot(-1) \cdot(-1))-(1 \cdot 2 \cdot 2)) \\ =-1((-2)+(2)+(-1)-(-1)-(1)-(-4)) \\ -1 \cdot((-6)+(2)-(3)-(8)) \\ -2 \cdot((-3)+(2)-(3)-(4)) \\ =-1(3)-1 \cdot(-15)-2 \cdot(-8) \\ =-3+15+16 \\ =28 \end{array} \)

Text erkannt:
\( A=\left(\begin{array}{cccc} 1 & 2 & 0 & -1 \\ 2 & 3 & -2 & 1 \\ -3 & 1 & 0 & -2 \\ 1 & -4 & 0 & 2 \end{array}\right), \quad B=\left(\begin{array}{cccc} 0 & 1 & 2 & -1 \\ 2 & -1 & -1 & -1 \\ 3 & -1 & -1 & 2 \\ 1 & -1 & -2 & 0 \end{array}\right), \quad \vec{f}=\left(\begin{array}{l} 1 \\ 2 \\ 0 \\ 0 \end{array}\right) \)
a) Berechnen Sie die Determinante der Matrizen \( A \) und \( B \) möglichst effizient.