Galois-Theorie; einführendes Beispiel

Question

Hallo zusammen!

Wir haben gerade Galois-Theorie und zu Beginn haben wir ein eInführendes Beispiel:

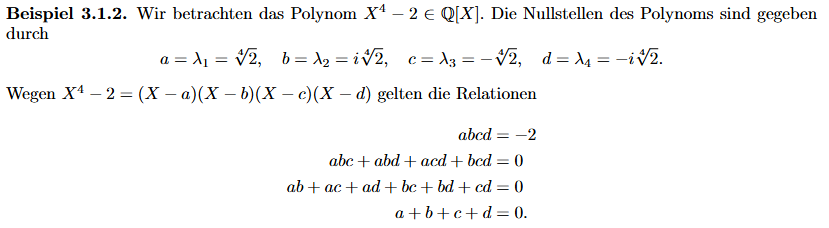
Meine Frage ist jetzt dazu, wieso man \(a^2b^2=-2;\: b^2c^2=-2;\: b^2c^2=-2;\: d^2a^2=-2\) (bzw. \(a^2c^2=2; b^2d^2\)) als Kanten (bzw. Diagonalen) eines Quadrats interpretieren kann?

Mir ist klar, dass a,b,c,d\(\in \mathbb{Q}\), aber warum dann aus dieser Gleichung sich ein geometrisches Quadrat zusammensetzen lässt, verstehe ich nicht...

Vielen Dank im Voraus!

Answer 1

Jede Kante des Quadrats kannst du lesen als: Die beiden Knoten, welche ich verbinde, erfüllen folgende Relation ... Je nachdem ob äussere Kante oder Diagonale, soll das Produkt der Knoten \(-2\) bzw \(2\) sein. Jetzt möchtest du alle Permutationen finden, welche diese Relationen erhalten, und das sind dann eben genau die Symmetrien des Quadrats (z.B. ist eine Permutation, welche \(c\) und \(d\) vertauscht, nicht erlaubt, da dann die Diagonale \(ac\) zu einer äusseren Kante wird).