Statistik Wahrscheinlichkeitsrechnung Maschinen

Question

Aufgabe:

Stimmen meine Ergebnisse? Weil bei der b) können die beiden Maschinen ja auch zeitgleich produzieren.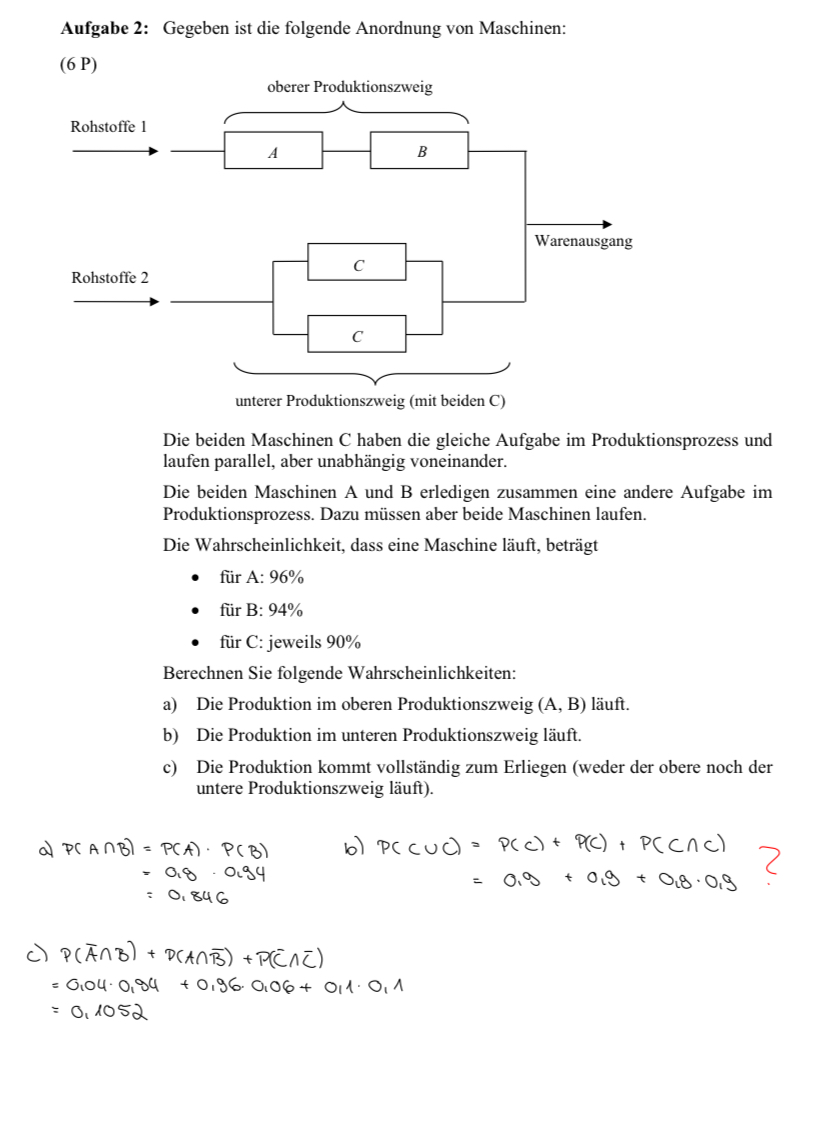

Text erkannt:

Aufgabe 2: Gegeben ist die folgende Anordnung von Maschinen:
(6 P)

Die beiden Maschinen C haben die gleiche Aufgabe im Produktionsprozess und laufen parallel, aber unabhängig voneinander.

Die beiden Maschinen A und B erledigen zusammen eine andere Aufgabe im Produktionsprozess. Dazu müssen aber beide Maschinen laufen.

Die Wahrscheinlichkeit, dass eine Maschine läuft, beträgt
- für \( \mathrm{A}: 96 \% \)
- für \( \mathrm{B}: 94 \% \)
- für C : jeweils \( 90 \% \)

Berechnen Sie folgende Wahrscheinlichkeiten:
a) Die Produktion im oberen Produktionszweig (A, B) läuft.
b) Die Produktion im unteren Produktionszweig läuft.
c) Die Produktion kommt vollständig zum Erliegen (weder der obere noch der untere Produktionszweig läuft).
\( \text { a) } \begin{aligned} P(A \cap B) & =P(A) \cdot P(B) & \text { b) } P(C \cup C) & =P(C)+P(C)+P(C \cap C) \\ & =0,8 \cdot 0,94 & & =0,9+0,9+0,8 \cdot 0,9 \\ & =0,846 & & \end{aligned} \)
\( \text { c) } \begin{aligned} & P(\bar{A} \cap B)+D(A \cap \bar{B})+P(\bar{C} \cap \bar{C}) \\ = & 0,04 \cdot 0,94+0,96 \cdot 0,06+0,1 \cdot 0,1 \\ = & 0,1052 \end{aligned} \)

Answer 1

Bei Aufgabe b) reicht es aber aus, wenn nur eine Maschine produziert.

Ich würde hier übrigens unterscheiden zwischen \(C_1\) und \(C_2\).

Dann gilt (übrigens auch ganz allgemein): \(P(C_1\cup C_2)=P(C_1)+P(C_2) \red{-}P(C_1\cap C_2)\).

Denn, dass beide Maschinen funktionieren, wird in der Summe bereits berücksichtigt und muss daher wieder abgezogen werden.

Teil c) stimmt nicht. Es fehlt der Fall, dass \(A\) und \(B\) nicht funktionieren. Und gesucht ist die Wahrscheinlichkeit, dass der erste Produktionsprozess und der zweite Produktionsprozess nicht funktionieren (weder ... noch). Da ist eine Wahrscheinlichkeit von 10 % sehr unrealistisch.

Comments

Text erkannt:

\( \text { a) } \begin{aligned} P(A \cap B) & =P(A) \cdot P(B) \\ & =0,8 \cdot 0,94 \\ & =0,846 \end{aligned} \)
b)
\( \begin{aligned} P(\subset \cup C) & =P\left(C_{1}\right)+P\left(C_{2}\right)-P\left(C_{1} \cap C_{2}\right) \\ & =0,9+0,9-0,8 \cdot 0,9 \\ & =0,99 \end{aligned} \)
c)
\( \begin{aligned} & P(\bar{A} \cap B)+D(A \cap \bar{B})+P(\bar{A} \cap \bar{B})+P\left(\bar{C}_{1} \cap \bar{C}_{2}\right) \\ = & 0,04 \cdot 0,94+0,96 \cdot 0,06 \cdot 0,04 \cdot 0,06+0,1 \cdot 0,1 \\ = & 0,1076 \end{aligned} \)

Ich habe es verbessert. Es sieht nun so aus. Stimmts?

---

b) passt jetzt, aber c) musst du dir noch einmal anschauen. :)

---

Text erkannt:

c) \( \begin{array}{l} P(\bar{A} \cap B)+D(A \cap \bar{B})+P(\bar{A} \cap \bar{B})+P\left(\bar{C}_{1} \cap \overline{C_{2}}\right) \\ = 0,04 \cdot 0,94+0,96 \cdot 0,06+0,04 \cdot 0,06+0,1 \cdot 0,1 \\ =0,1292\end{array} \)

---

Beachte den zweiten Teil zu c) in meiner Antwort. Gesucht ist die Wahrscheinlichkeit, dass beide Produktionsprozesse gleichzeitig nicht funktionieren und nicht, dass mindestens irgendeine Maschine nicht funktioniert.

Answer 2

a) P(ober Produktionszweig läuft) = 0.96·0.94 = 0.9024

b) P(unterer Produktionszweig läuft) = 1 - (1 - 0.9)·(1 - 0.9) = 0.99

c) P(beide Produktionszweige laufen nicht) = (1 - 0.9024)·(1 - 0.99) = 0.000976