Definitionslücken, Polstellen und Asymptoten bei gebrochenrationalen und Exponentialfunktionen

Question

1-) Skizzieren Sie ohne Verwendung eines GTR den groben Verlauf des Graphen der Funktion \( f \) mit \( f(x)=\frac{e^{x}}{(x-3)^{2}} \) mithilfe von Teilfunktionen.

2-) Geben Sie jeweils die Definitionslücken der Funktion an und prüfen Sie, ob es sich um einen Pol mit bzw. ohne Vorzeichenwechsel handelt.
a) \( f(x)=\frac{x}{x+1} \)
b) \( f(x)=\frac{x^{2}-4}{x-3} \)
c) \( f(x)=\frac{x^{4}+1}{x^{3}} \)
d) \( f(x)=\frac{x^{2}-6 x+9}{x^{2}+2 x+1} \)

3-) Geben Sie die Polstellen und die Asymptote der Funktion \( f \) an.
a) \( f(x)=\frac{2}{x-3}+4 \)
b) \( f(x)=2 x+\frac{2}{x+2} \)
c) \( f(x)=\frac{1}{x^{2}-10 x+25} \)
d) \( f(x)=\frac{2 x+3}{x(x+1)}+\frac{x}{2} \)

Comments

Kannst du auch sagen, was genau dir Schwierigkeiten bereitet?

Answer 1

Definitionslücken sind Nullstellen des Nenners. Wenn diese nicht gleichzeitig Nullstellen des Zählers sind, sind es Polstellen. Ihre Häufigkeit (gerade/ungerade) entscheidet über den Vorzeichenwechsel.

Answer 2

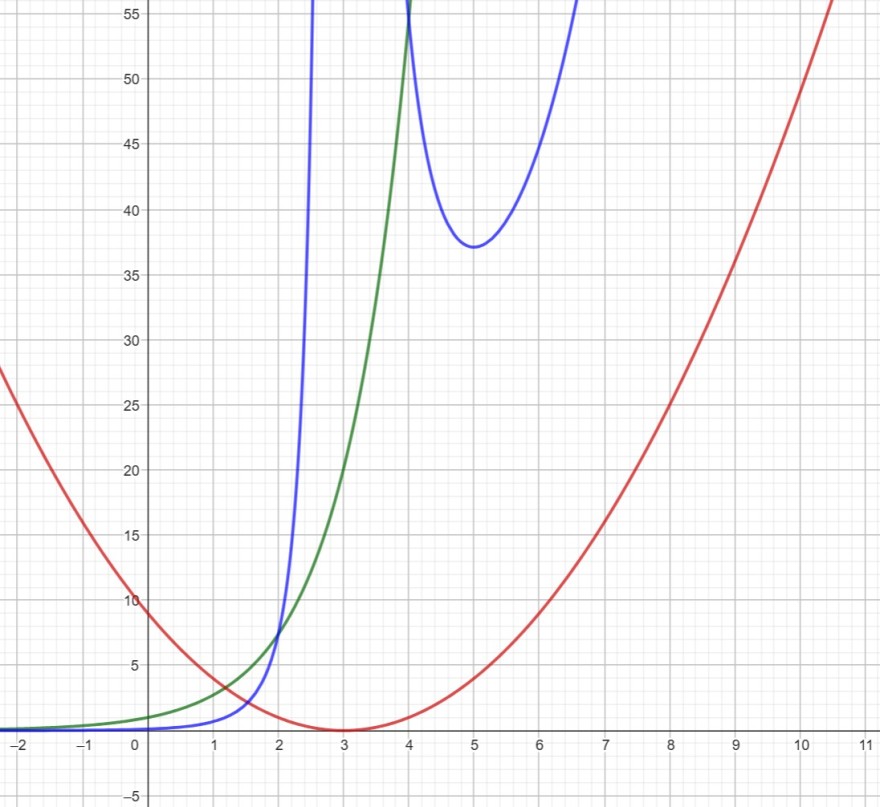
1. Skizzieren Sie ohne Verwendung eines GTR den groben Verlauf des Graphen der Funktion f(x) = e^{x}/(x - 3)^{2} mithilfe von Teilfunktionen.

Zeichne die Funktion des Zählers und des Nenners. Bei mir grün und rot und bilde dann daraus den Quotienten und skizziere ihn ein.

Dabei brauchst du die y-Achse nicht mit Werten beschriften und es muss auch nicht exakt sein. Man sollte nur erkennen können wie der blaue Graph grundsätzlich verläuft.

Comments

2. a)

Der Nenner x + 1 hat bei -1 eine einfache Nullstelle mit Vorzeichenwechsel. Der Zähler nimmt bei x = -1 den Wert -1 ≠ 0 an. Damit ist -1 eine Definitionslücke/Polstelle mit Vorzeichenwechsel.