Aufgabe:
2.1 Berichtigen Sie die vorgegebenen falschen Aussagen und begründen Sie:
a) Die trigonometrische Funktion \( \mathrm{f}(\mathrm{x})=\sin \mathrm{x} \) ist achsensymmetrisch.
b) Die trigonometrische Funktionen \( \mathrm{f}(\mathrm{x})=\sin \mathrm{x} \) hat fur \( \mathrm{x} \in \mathbb{R} \) genau drei Nullstellen.
c) Die trigonometrische Funktion \( \mathrm{f}(\mathrm{x})=\sin \mathrm{x} \) ist im Intervall \( 0 \leq \mathrm{x} \leq 2 \pi \) streng monoton wachsend.
d) Die trigonometrische Funktion \( f(x)=\sin x \) hat genau eine Asymptote.
e) Die trigonometrische Funktion \( f(x)=\cos x \) hat den Wertebereich \( -1<y<1, x \in \mathbb{B} \).
f) Die trigonometrische Funktionen \( \mathrm{f}(\mathrm{x})=\cos \mathrm{x} \) hat fur \( \mathrm{x} \in \mathbb{R} \) genau zwei Nullstellen \( \leq \pi \)
g) Die trigonometrische Funktion \( f(x)=\cos x \) hat eine Asymptote fur \( y=1 \).
2.2 Stellen Sie folgende Funktion \( \mathrm{f} \) in jeweils einem geeigneten Koordinatensystem grafisch dar!
a) \( f(x)=2 \sin (2 x+3 \pi),-\pi \leq x \leq \pi \)
b) \( f(x)=3 \sin \left(0,5 x-\frac{\pi}{4}\right),-\pi \leq x \leq 4 \pi \)
c) \( f(x)=\frac{7}{2} \cdot \sin \left(\frac{2}{3} \cdot x+\frac{\pi}{6}\right) ; 2 \pi \leq x \leq 4 \pi \)
d) \( f(x)=2 \sin \left(\frac{1}{2} x+\frac{\pi}{4}\right) ;-2 \pi \leq x \leq 3 \pi \)
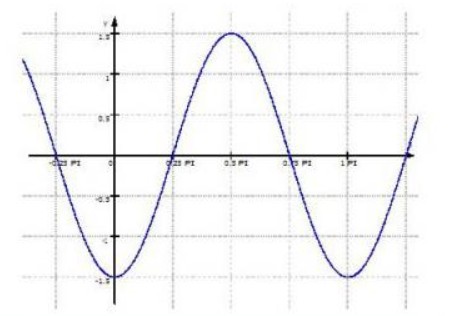
2.3 Die Abbildung zeigt den Graphen einer Funktion \( \mathrm{f}(\mathrm{x})=\mathrm{a} · \sin (\mathrm{b} \mathrm{x}+\mathrm{c}) \).
Geben Sie zwei mögliche Funktionsgleichungen an.