Betrachten Sie folgende Differentialgleichung \( (x \in \mathbf{R}) \) :
\( \frac{\mathrm{d}}{\mathrm{d} t} x=-x^{3}+x a \)
a) Berechnen Sie alle Fixpunkte \( x^{*} \) der DGL für \( a=4 \) und bestimmen Sie deren Stabilität.
b) Lösen Sie die Unteraufgabe (a) für beliebige \( a \in \mathbf{R} \).
c) Zeichnen Sie die Fixpunkte als Funktion des Parameters \( a: x^{*}=f(a), a \in \mathbf{R} \). Verwenden Sie dabei für stabile Fixpunkte durchgezogene Linien und für instabile Fixpunkte gestrichelte Linien.
Ansatz:
Ich würde die Zahlen einsetzen und dann ableiten, aber es kann nur nach t abgeleitet werden, also kann man gar nicht ableiten, oder?
-x³+xa
-x³+x*4
-3x²+4
instabil (Graph geht nach unten)
zu a) -3x²+4
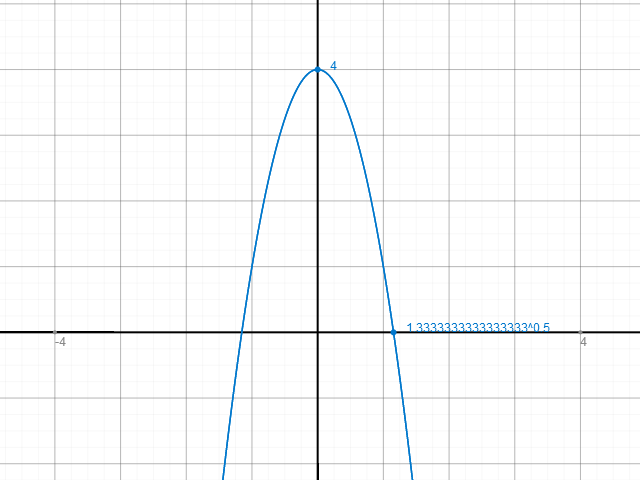
zu b)
Je größer a ist desto weiter steigt die umgekehrte Parabel auf der y-Achse nach oben und umso kleiner bzw. negativer a ist z.B. -10 desto weiter sinkt die umgekehrte Parabel auf der y-Achse nach unten.
a∈ℝ
