Aufgabe:
Zeichne die folgenden Paare von Vektoren in einem \( x y \) -Koordinatensystem. Addiere die Vektoren (arithmetisch), zeichne den resultierenden Vektor und berechne seine Länge:
a) \( \vec{A}=[0,4], \vec{B}=[3,0] \);
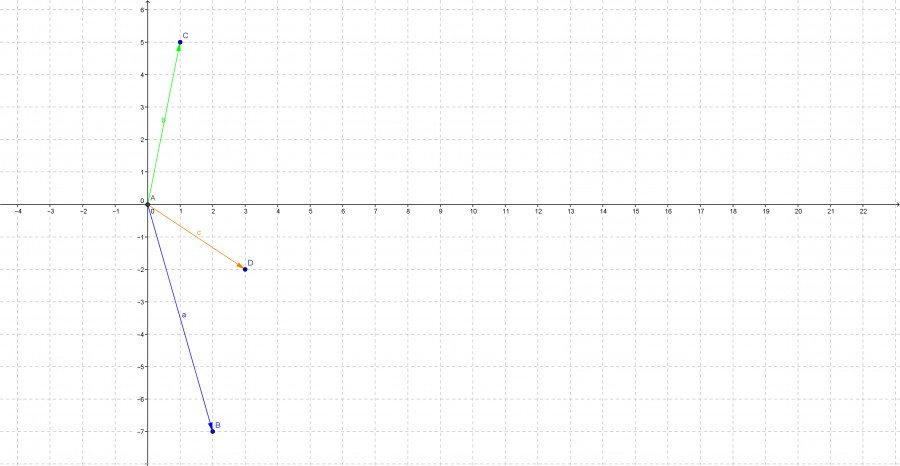
b) \( \vec{A}=[2,-7], \vec{B}=[1,5] \);
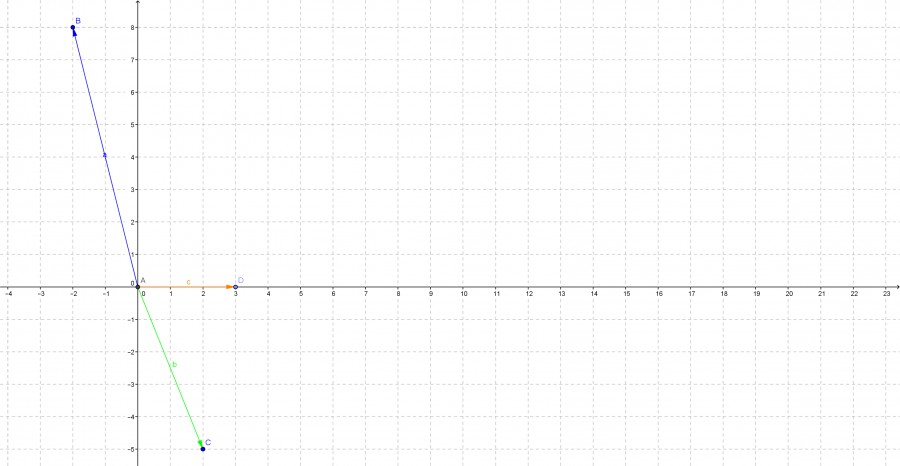
c) \( \vec{A}=[-2,8] ; \vec{B}=[2,-5] \)
Unten sind meine Lösungen, weiß aber nicht, ob ich es richtig berechnet habe.
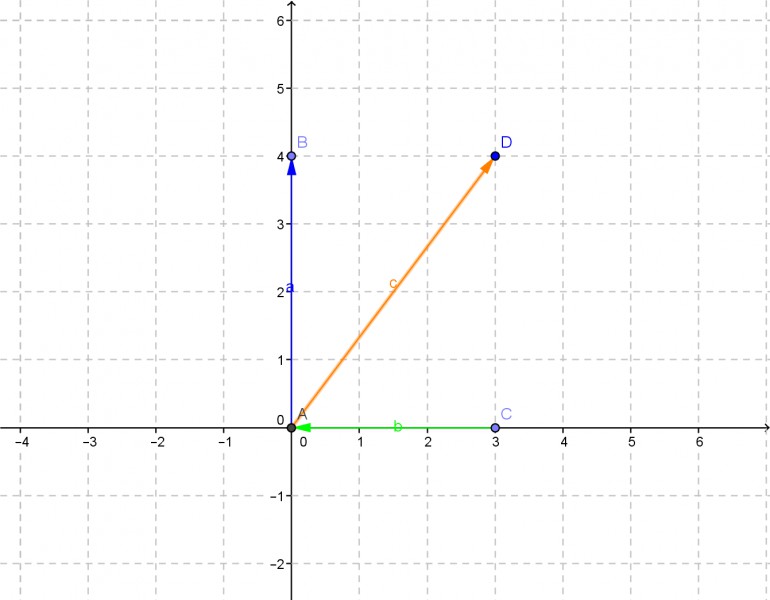
a) \( \vec{a}=\left(\begin{array}{l}0 \\ 4\end{array}\right) \)
\( \overrightarrow{|a|}=\sqrt{0^{2}+4^{2}}=4 \)
\( \vec{b}=\left(\begin{array}{l}3 \\ 0\end{array}\right) \)
\( \overrightarrow{|b|}=\sqrt{3^{2}+0^{2}}=3 \)
\( \vec{c}=\overrightarrow{|a|}+\overrightarrow{|b|} \)
\( \vec{c}=4+3=7 \quad L E \)
b) \( \vec{a}=\left(\begin{array}{c}2 \\ -7\end{array}\right) \)
\( \overrightarrow{|a|}=\sqrt{2^{2}+(-7)^{2}}=\sqrt{53} \)
\( \vec{b}=\left(\begin{array}{l}1 \\ 5\end{array}\right) \)
\( \overrightarrow{|b|}=\sqrt{1^{2}+5^{2}}=\sqrt{26} \)
\( \vec{c}=\overrightarrow{|a|}+\overrightarrow{|b|} \)
\( \vec{c}=\sqrt{53}+\sqrt{26}=\sqrt{89} \quad L E \)
c) \( \vec{a}=\left(\begin{array}{c}-2 \\ 8\end{array}\right) \)
\( \overrightarrow{|a|}=\sqrt{(-2)^{2}+(8)^{2}}=\sqrt{68} \)
\( \vec{b}=\left(\begin{array}{c}2 \\ -5\end{array}\right) \)
\( \overrightarrow{|b|}=\sqrt{2^{2}+(-5)^{2}}=\sqrt{29} \)
\( \vec{c}=\overrightarrow{|a|}+\overrightarrow{|b|} \)
\( \vec{c}=\sqrt{68}+\sqrt{29}=\sqrt{97} \quad L E \)