Beweise am Einheitskreis: (sin(40°))^2 + (cos(40°))^2 = 1

Question

Wer kann mir helfen? Beweise am Einheitskreis: (sin(40°) )^2 + (cos(40°))^2 = 1

b)  Zeige an einem beliebigen rechtwinkligen Dreieck mit y = 90° : (sin(a) )^2 + (cos(a) )^2 = 1

hinter den Klammern ist hoch 2 gemeint

Answer 1

zu a)

 

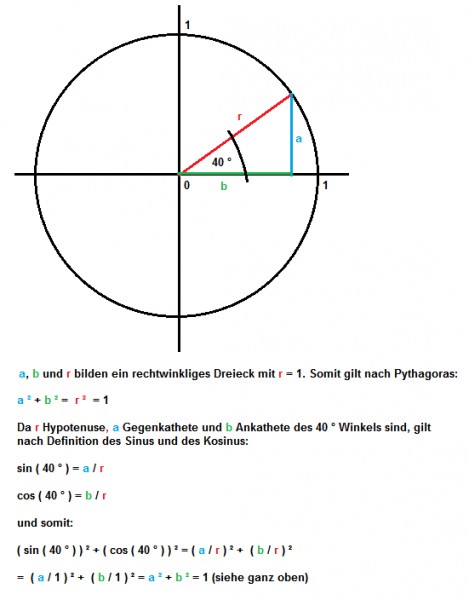
zu b)

Die obige Argumentation gilt für jede Winkelgröße, nicht nur für einen 40 °-Winkel.

Da es zu jedem rechtwinkligen Dreieck ein ähnliches Dreieck mit Hypotenusenlänge 1 gibt und in ähnlichen Dreiecken die Längenverhältnisse einander entsprechender Seiten gleich sind, gilt die obige Argumentation also auch für jedes beliebige, rechtwinklige Dreieck.

Somit gilt in einem beliebigen, rechtwinkligen Dreieck für jeden beliebigen Winkel alpha die Behauptung:

( sin ( alpha ) ) ² + ( cos ( alpha ) ) ² = 1