Eigenschaften des Graphen aus einer Parabelgleichung ablesen

Question

Gegeben ist die Funktion f mit f(x) = -x^2 - 6x - 5

wie sind da die Graphen ?

 

Danke für die Hilfe im voraus :)

Comments

machst du auch gerad quadratische gleichungen?

---

Jap ^^ Hausaufgaben..

Answer 1

 f(x) = -x^2 - 6x - 5

hat nur einen Graphen. 

Wie weiss man, wie er aussieht?

Der Grad der Funktionsgleichung ist 2. Darum Parabel.

-x^2: Form: Nach unten geöffnete Normalparabel

Nullstellen?

f(x) = -x^2 - 6x - 5 = - (x^2 + 6x + 5)         |faktorisieren:

     = - (x+5)(x+1)

Nullstellen: x1 = -5, x2 = -1

Scheitelpunkt?

Genau zwischen den Nullstellen.

Also x_S = (-5 + (-1)) / 2 = - 3

y_s = -(-3)^2 - 6*(-3) - 5 = -9 + 18 – 5 = 4

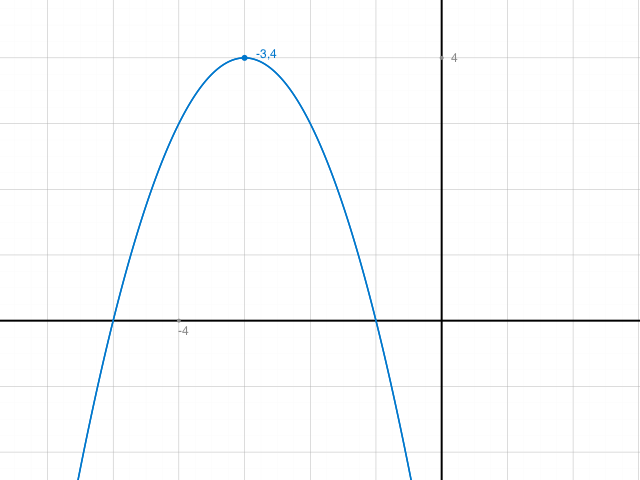
So sieht der Graph aus: (ein Ausschnitt):

 

Comments

https://www.mathelounge.de/11248/quardraitische-gleichungen LU kannst du mir das auch beantworten ?