An sich ist das eine Aufgabe der Variationsrechnung (falls dich das näher interessiert, nachschlagen kann man das z.B., wenn man nach "Lagrange-Formalismus", "Hamilton-Formalismus" oder einfach "Variationsrechnung" googelt) allerdings ist das mehr oder weniger kompliziert.
Etwas einfacher wird es, wenn man als bekannt Voraussetzt, dass die kürzeste Verbindung zweier Punkte auf der Gerade zwischen beiden liegt.
Dann kann man nämlich ausnutzen, dass für den Abstand eines Punktes P(a,b) von einem beliebigen Punkt auf der Funktion f(x)=y nach dem Satz des Pythagoras
$$ d ( x , y ) = \sqrt { ( x - a ) ^ { 2 } + ( y - b ) ^ { 2 } } = \sqrt { ( x - a ) ^ { 2 } + ( f ( x ) - b ) ^ { 2 } } $$
gilt, der Abstand wird also eine reine Funktion in x.
Damit diese ein Extremum hat, muss
d'(x)=0 gelten.
Da es einfacher zu rechnen ist, kann man auch die Funktion D(x) = d(x)2 betrachten: man kann sich leicht überlegen, dass sie an den gleichen Stellen Extrema hat, die d(x). Im Nachhinein muss man dann nur noch überlegen, ob es sich um Minima oder Maxima von d(x) handelt.
Untersuche also D'(x)=0:
$$ \begin{array} { l } { 0 = D ^ { \prime } ( x ) = \left( ( x - a ) ^ { 2 } + ( f ( x ) - b ) ^ { 2 } \right) ^ { \prime } = 2 ( x - a ) + 2 ( f ( x ) - b ) ^ { * } f ^ { \prime } ( x ) } \\ { 0 = 2 x + 2 f ( x ) f ^ { \prime } ( x ) - 2 b ^ { * } f ^ { \prime } ( x ) - 2 a } \end{array} $$
Diese Gleichung muss nun (für gegebenes f(x), sowie gegebenes a und b) nach x gelöst werden, dann hat man die x-Koordinaten aller Punkte auf f, die einen extremalen Abstand zu P(a,b) haben.
Beispiel:
Nehmen wir eine Gerade, z.B. f(x) = 2x+1, der Punkt ist (1, 1).
f(x) = 2x+1, f'(x) = 2, a=b=1:
0 = 2x+2*(2x+1)*2-2*1*2-2*1=2x+8x+4-4-2=10x-2
x = 1/5
Der nächste Punkt zu P auf f hat also die x-Koordinate 1/5. Setzt man diese in d(x) = sqrt(D(x)) ein, so erhält man:
d(x) = sqrt((1/5-1)^2+(2/5-1+1)^2) = 2/sqrt(5)
Zeichnet man sich das ganze mal auf, so erhält man:
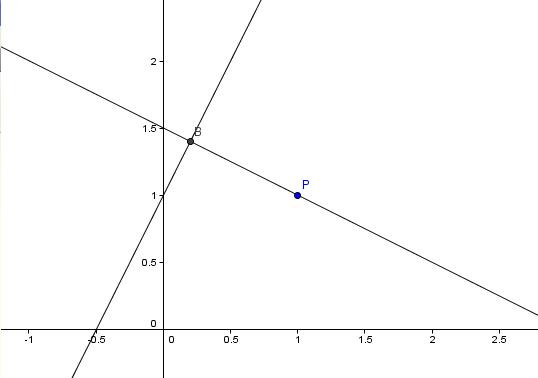
Der Abstand liegt also auf der Senkrechten zur Gerade, wie es auch zu erwarten war.
Für kompliziertere Funktionen ist der Ablauf natürlich etwas komlexer, an sich ändert sich aber nichts an der Vorgehensweise.