eine quadratische Funktion hat die allgemeine Form
f(x) = ax2 + bx + c
Gegeben ist, dass nach 0 Sekunden der Stein eine Höhe von 1,50 Metern hat, also
f(0) = a*02 + b*0 + c = 1,50 | also c = 1,50
Nach zwei Sekunden erreicht der Stein seine maximale Höhe von 4,50 Metern, also
f(2) = a*22 + b*2 + 1,50 = 4,50
Und da es die maximale Höhe ist, muss bei x = 2 auch die 1. Ableitung der Funktion = 0 sein, also
f'(x) = 2ax + b
f'(2) = 4a + b = 0
Damit haben wir drei Gleichungen mit 3 Unbekannten:
I. c = 1,50
II. 4a + 2b = 3
III. 4a + b = 0
a = -0,75
b = 3
c = 1,5
a)
Die Gleichung lautet also
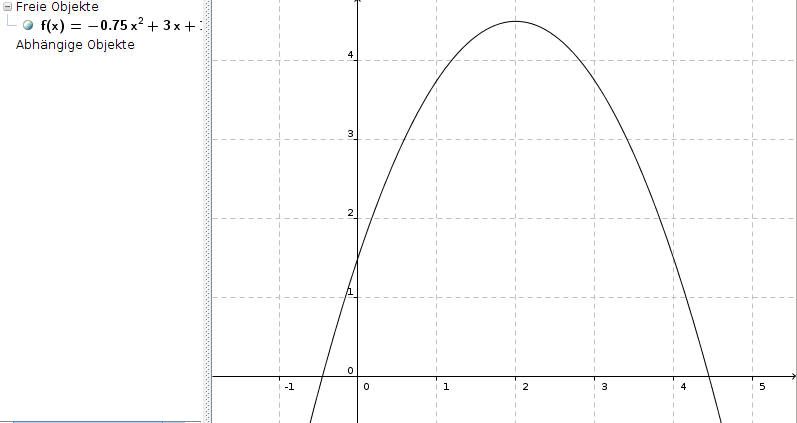
f(x) = -0,75x2 + 3x + 1,5
b)
Nach wie viel Sekunden fällt der Stein ins Wasser?
f(x) = -0,75x2 + 3x + 1,5 = 0 | : (-0,75)
x2 - 4x - 2 = 0 | pq-Formel
x1,2 = 2 ± √(4 + 2) = 2 ± √6
x1 ≈ 4,45
x2 ≈ -0,45
Eine negative Zeit ist unsinnig, also fällt der Stein nach ca. 4,45 Sekunden ins Wasser.
Besten Gruß