Die Ausgangsfunktion ist gegeben f(x)=0,5x^3 - 4,5x^2 + 12·x - 9.
Die Abbildung 1 zeigt den zu f gehörigen Graphen.
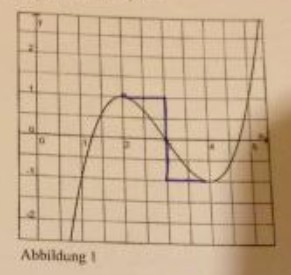
a) Weisen Sie rechnerisch nach, dass der Graph von f in H(2, 1) einen Hochpunkt und in T(4, 1) einen Tiefpunkt besitzt.
b) Die Funktion \( f \) lässt sich auch darstellen in der Form:
\( f(x)=(x-3) \cdot\left(0,5 \cdot x^{2}-3 \cdot x+3\right) \)
Ermitteln Sie alle Nullstellen von f und geben Sie diese nicht als Näherungswerte, sondern exakt an.
c) Zeigen Sie, dass der Graph von f den Wendepunkt W(3|0) besitzt. Bestimmen Sie eine Gleichumg der Wendetangente an den Graphen von f.
d) Entscheiden Sie, ob die Aussagen A bis C jeweils wahr oder falsch sind. Begründen Sie Ihre Entscheidungen.
A: Die Steigung der Geraden durch die Punkte \( T(4|-1) \) und \( A(6| f(6))) \) beträgt 5.
B: Der Graph der Ableitungsfunktion \( f' \) fällt für \( x>3 \).
C: Die Funktionswerte der Ableitung von \( f \) sind nie kleiner als \( -1,5 \).