Erstmal Danke für diese Seite, jetzt weiß ich wo ich fragen kann, wenn ich was nicht verstehe ;)
Und ich entschuldige mich schonmal für meine übertrieben ausführliche Frage, aber so bin ich, anders kann ich es nicht nachvollziehen und hoffe, mir kann das einer auch ausfürhlich genug erklären :)
Nun denn, hier die Aufgabe: Von einer rechteckigen Platte ist an einer Ecke ein Stück abgebrochen. Aus dieser Restplatte soll wieder ein rechteckiges Stück mit möglichst großer Fläche geschnitten werden. Wie groß sind dabei die Seiten zu wählen?
Zur Veranschaulichung ein Bild von mir mit Paint mal eben schnell skizziert (Sorry falls es doof aussieht):
Hier nochmal die Erklärung zum Bild:
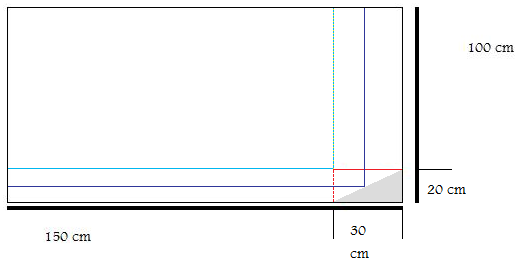
Die Platte soll das ganz große Rechteck sein, welches ich mit einem schwarzen dünnen Rand eingezeichnet habe. Daneben bzw. darunter sind die Maße (Die Platte ist insgesamt 150 cm (Breite) * 100 cm (Höhe) groß) angegeben.
Unten rechts habe ich das abgebrochene Stück hellgrau makiert. Nun wollte ich fragen, ob mein Denkweg und eventuell sogar auch meine Funktion, die ich ja benötige um einen Extremwert zu bekommen, richtig sind:
Erst habe ich nur gedacht: Einfache Aufgabe, da rechne ich einfach die abgebrochene Stelle mal 2 und ziehe sie dann von der vorherigen Gesamtfläche ab. Anfangs habe ich auch nur 2 Möglichkeiten gesehen, eine rechteckige Platte "wiederherzustellen". Ich habe mir gedacht, die Platte kann entweder nur (100cm-20cm) * 150 cm, oder (150cm-30cm) * 100 cm sein. Erst später habe ich gemerkt, dass diese Überlegung quatsch ist und dann habe ich eine von vielen weiteren Möglichkeiten gesehen, die es gibt.
Wie man an der dunkelblauen Linie erkennen kann, kann der Schnitt auch so gemacht werden, um die Platte wieder in eine rechteckige zu verwandeln.
So nun zu meiner Rechnung:
Ziel: Größte Fläche, wobei der Mindestflächeninhalt 80cm*150cm oder 120cm*100cm (beides ergibt 12000 cm2) groß ist. Jetzt gilt es zu überprüfen, ob es einen noch größeren möglichen Flächeninhalt gibt.
Ich habe eine Funktion aufgestellt, in der die Bereiche 0-20 für mich eine Rolle spielen:
Allgemein: x * y = Flächeninhalt
Für meine Aufgabe:
f(x) = (100-x) * (150+ (-30+30*(x/20)))
Heraus käme ja der Flächeninhalt.
Ich habe diese Funktionsgleichung (bezogen auf die sich ergebenden Maße an einem gewählten Punkt auf der abgebrochenen Stelle) herausentnommen, weiß jedoch nicht ob ich y zu x richtig in Beziehung gesetzt habe. Ich wollte wissen, ob es der richtige Weg ist oder ob ihr einfacher vorgegangen wärt.
Falls die Funktion richtig ist, weiß ich wie ich weitermachen muss (1. Ableitung usw.)
Falls keiner von euch mich versteht, sry ich kann mich nie so wirklich richtig gut ausdrücken... Hoffe mir kann jemand helfen, ansonsten