Wurzelgleichung lösen: √(x + 2) + 1 = √(2x + 2)

Question

Kann man eine Wurzelgleichung nur durch Äquivalenzumformung lösen?

Bestimmen Sie die Lösungsmenge der Gleichung \( \sqrt{x+2}+1=\sqrt{2 x+2} \) in den reellen Zahlen.

Answer 1

 

vielleicht so:

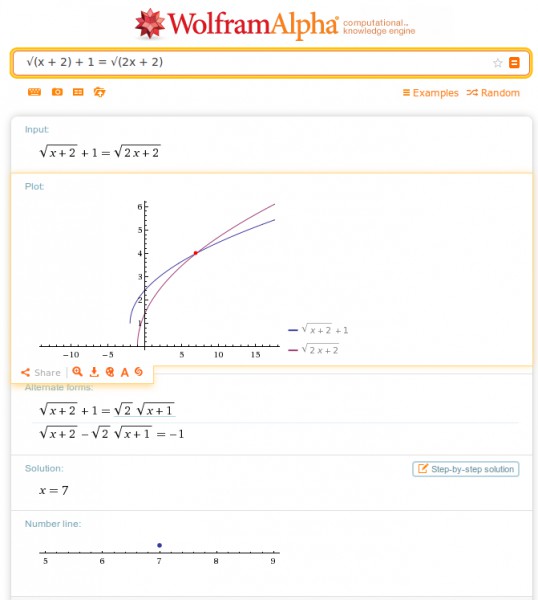
√(x + 2) + 1 = √(2x + 2) | Quadrieren

(x + 2) + 2 * √(x + 2) + 1 = 2x + 2 | - x - 2 - 1

2 * √(x + 2) = 2x + 2 - x - 2 - 1 = x - 1 | : 2

√(x + 2) = (x - 1) / 2 | Quadrieren

x + 2 = (x - 1)² / 4

x + 2 = x²/4 - 2x/4 + 1/4 | * 4

4x + 8 = x² - 2x + 1

x² - 6x - 7 = 0 | pq-Formel

x_1,2 = 3 ± √(9 + 7)

x₁ = 7

x₂ = -1

 

Probe:

√9 + 1 = √16 | stimmt

√1 + 1 = √0 | stimmt nicht

 

Da das Quadrieren keine Äquivalenzumformung ist, bleibt also als einzige Lösung der Gleichung:

x = 7

Besten Gruß