Symmetrieverhalten von Kurven bei Funktionen. Beispiel y=4x²-16

Question

Wie erkenne ich das Symmetrieverhalten von y=4x²-16

In der Lösung steht gerade aber ich habe gedacht wenn x² vorkommt handelt es sich immer um eine Kurve ?

Answer 1

 

f(x) = y = 4x² - 16

 

Du hast Recht: Der Graph von f(x) ist eine "Kurve":

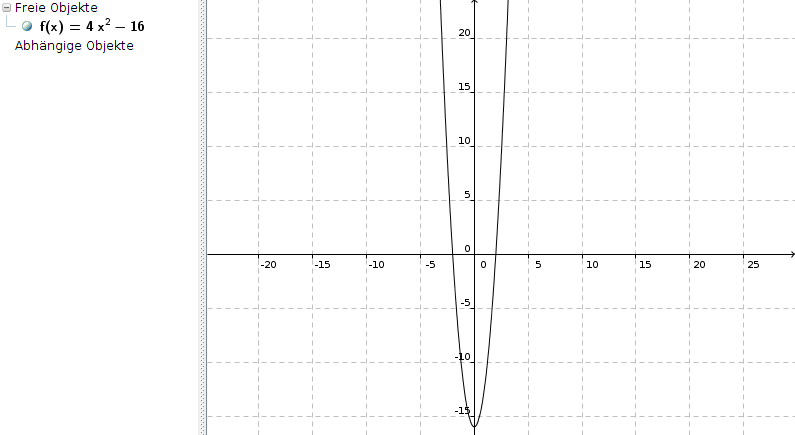
Das Wort "gerade" bezieht sich aber auf das Symmetrieverhalten der Funktion bzw. des Graphen:

Wir haben nur gradzahlige Exponenten von x, nämlich 2 (in x²) und 0 (in 16*x⁰ = 16*1 = 16).

Dadurch ist der Graph achsensymmetrisch zur y-Achse:

f(x) = f(-x) für alle x.

 

Ungerade und damit punktsymmetrisch zum Urspruch wäre dagegen zum Beispiel die Funktion

f(x) = x³ - x

 

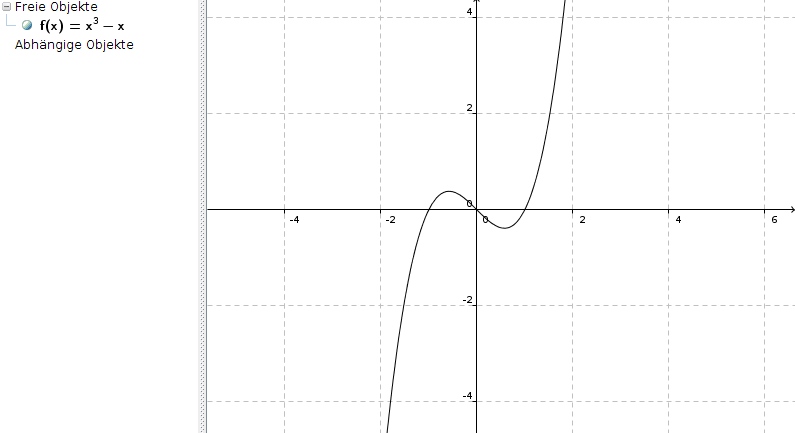
Wenn Du ein Gemisch aus geraden und ungeraden Exponenten hast wie zum Beispiel

f(x) = x² - x

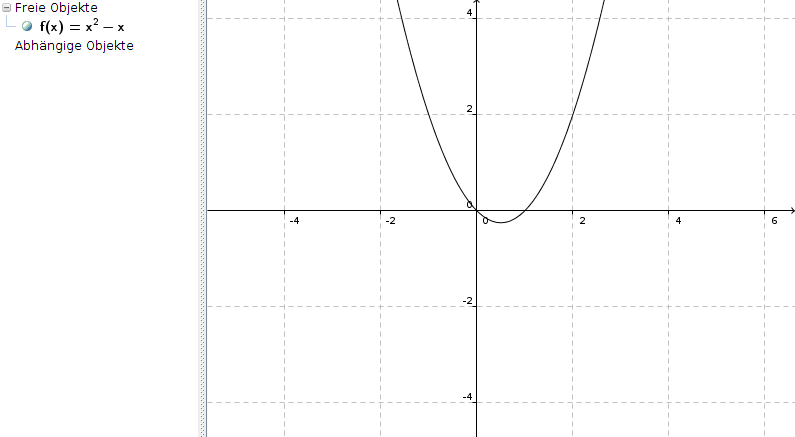
dann hast Du weder Achsensymmetrie zur y-Achse noch Punktsymmetrie zum Ursprung.

 

Besten Gruß

Answer 2

f(x) = 4x²-16

Symmetrieverhalten wird untersucht, wenn man in die Funktion ein negatives Argument einsetzt und schaut, ob ein Funktionswert mit welchem Vorzeichen rauskommt.

Bei f(x) = f(-x) -> Achsensymmetrie

Bei f(x) = - f(-x) -> Punktsymmetrie

f(-x) = 4*(-x)² -16 = 4x²-16 -> f(x) = f(-x) -> Es liegt eine Achsensymmetrie vor.