Die Nullstellenberechnung habe ich ansatzweise schon im Kommentar
angeführt. Falls nicht klar dann bitte melden.
Vorüberlegung : die Funktion ist achsensymmetrisch, da nur
gerade Hochzahlen vorkommen.
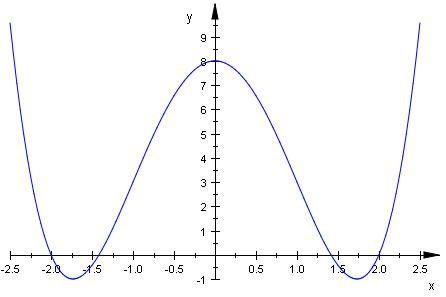
f ( x ) = x4 - 6 * x2 + 8
1.Ableitung
f ´ ( x ) = 4 * x3 - 12 * x
Extremstellen
x * ( 4 * x2 - 12 ) = 0
x = 0
4 * x2 - 12 = 0
x = √ 3
x = - √ 3
f ( 0 ) = 8
f ( √ 3 ) = ( √ 3 )^4 - 6 * ( √ 3 )^2 + 8 = -1
E ( 0 | 8 )
E ( √ 3 | -1 )
E ( -√ 3 | -1 )
2.Ableitung
f ´´ ( x ) = 12 * x^2 - 12
Wendepunkte
12 * x^2 - 12 = 0
x = +1
x = -1
W ( ±1 | 3 )
Wendetangenten
Steigung im Wendepunkt
f ´ ( 1 ) = 4 * 1^3 - 12 * 1 = -8
y = m * x + b
3 = -8 * 1 + b
b = 11
Wendetangente x = 1
t ( x ) = -8 * x + 11
Wendetangente x = -1
t ( x ) = 8 * x + 11
b.)
Die Wendetangente im Hochpunkt ist eine Parallele
zur Achse als Funktion h ( x ) = 8
Als weiterer Schnittpunkt mit dem Graph ergibt sich
f ( x ) = x4 - 6 * x2 + 8 = 8
x4 - 6 * x2 = 0
hier auch wieder ersetzen
z = x^2
z^2 - 6 * z = 0
z * ( z - 6 ) = 0
Ein Produkt ist dann gleich 0 wenn mindestens einer der Faktoren 0 ist
z = 0 | bekannt
z - 6 = 0
z = 6
x^2 = 6
x = √ 6
Stammfunktion bilden
∫ f ( x ) = ∫ x4 - 6 * x2 + 8 dx
x^5 / 5 - 6 * x^3 / 3 + 8 *x
So, das wars weil ich jetzt noch was erledigen muß.
Du mußt dir jetzt anhand der Skizze überlegen welche
( Teil- ) Fläche gemeint ist, was Abzugsflächen sind usw.
Bei Fehlern oder Fragen wieder melden.
Bin gern weiterhin behilflich.
mfg Georg