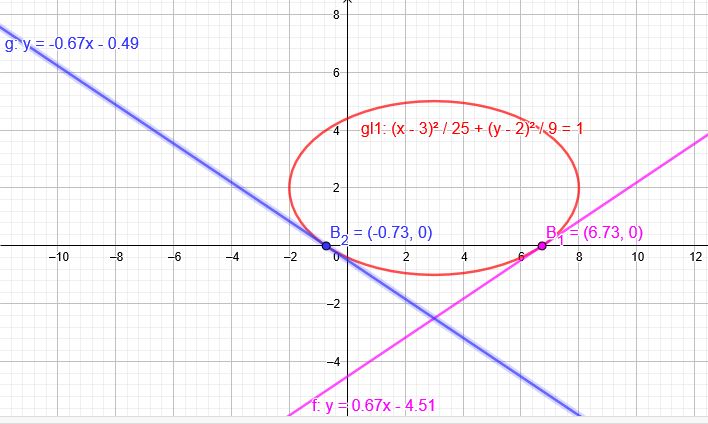
Eine Ellipse hat den Mittelpunkt \(M (3|2)\) und die Halbachsen \(a = 5 cm\) und \(b= 3 cm\)
\( \frac{(x-3)^2}{25}+\frac{(y-2)^2}{9} =1\)
b) Wie lauten die Tangentengleichungen an die Ellipse bei den Punkten, an welchen die Ellipse die x-Achse schneidet?
Schnitt mit der x-Achse: \(y=0\)
\( \frac{(x-3)^2}{25}+\frac{(0-2)^2}{9} =1\)
\( (x-3)^2 =\frac{125}{9}\)
1.) \( x=\frac{5}{3}\cdot\sqrt{5}+3\)
\( f(x,y)=\frac{(x-3)^2}{25}+\frac{(y-2)^2}{9} -1\)
\( \frac{df(x,y) }{dx}=\frac{2\cdot(x-3)}{25}\)
Tangentensteigung: \(m_1= \frac{2\cdot(\frac{5}{3}\cdot\sqrt{5}+3-3)}{25}= \frac{2\cdot(\frac{5}{3}\cdot\sqrt{5})}{25}=\frac{2}{15}\cdot\sqrt{5}\)
2.) \( x=-\frac{5}{3}\cdot\sqrt{5}+3\)
Tangentensteigung:
\( m_2=\frac{2\cdot(-\frac{5}{3}\cdot\sqrt{5}+3-3)}{25}=\frac{2\cdot(-\frac{5}{3}\cdot\sqrt{5})}{25}=-\frac{2}{15}\cdot\sqrt{5}\)
Nun die Tangentengleichungen aufstellen.