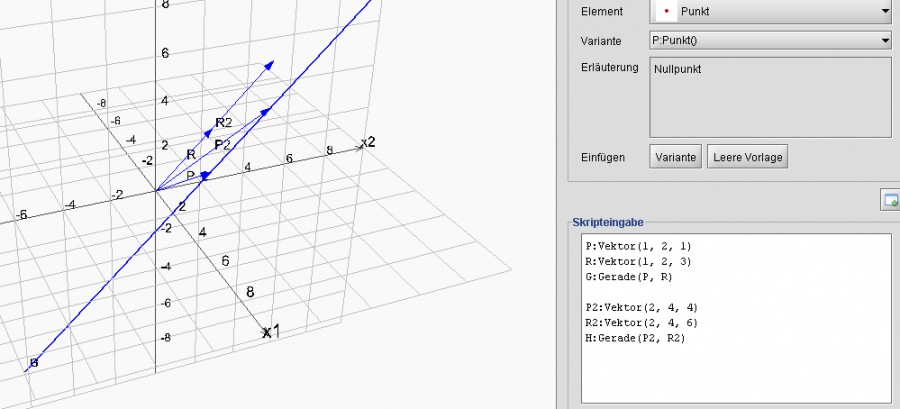
Also wenn die deckungsgleiche Gerade h ein Vielfaches des Richtungsvektors von g hat, sind sie ja parallel. Wenn der Ortsvektor von h dann noch gleich dem von g ist, sind sie deckungsgleich.
Schau
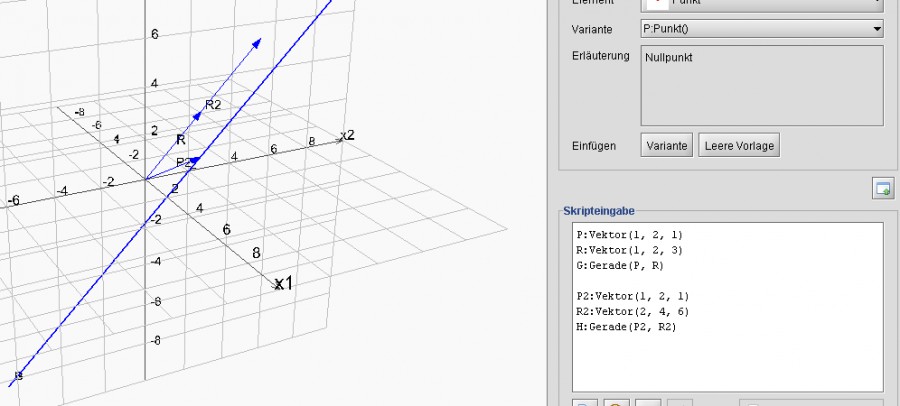
Jetzt steht in der Aufgabenstellung aber, dass g und h verschiedene Ortsvektoren haben sollen. Jetzt kann man den Ortsvektor von h aber nicht irgendwo hin verschieben, weil h sonst die Deckung mit g verlieren würde, also so würde das aussehen, wenn ich den Ortsvektor von h einfach auf (1,5,1) setzen würde. Dann wären g und h zwar parallel, aber nicht deckungsgleich.
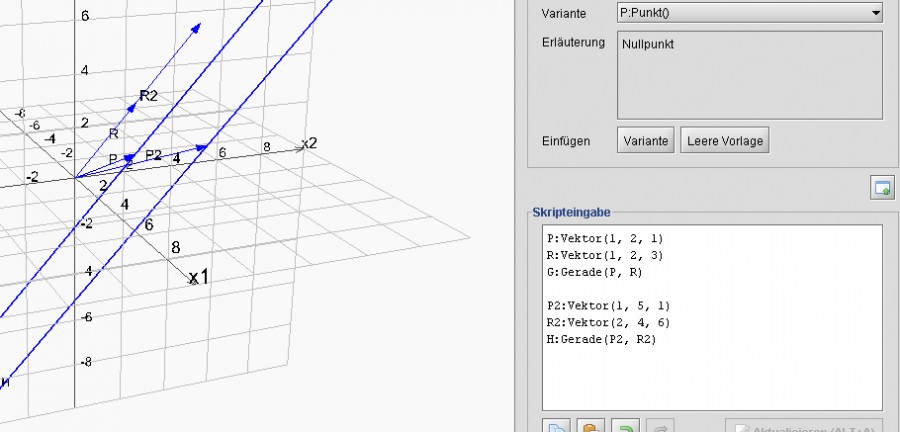
Also muss ich den Ortsvektor entlang des Richtungsvektors verschieben, indem ich ein Vielfaches vom Richtungsvektor auf den Ortsvektor addiere, z.B. (1,2,1) + 1*(1,2,3) = (2,4,4), dann sind sie immernoch deckungsgleich, trotz verschiedener Orts- und Richtungsvektoren: