Nun, die allgemeine Funktionsgleichung einer Polynomfunktion vom Grad 3 ist :
f ( x ) = a x 3 + b x 2 + c x + d
Die Ableitung ist:
f ' ( x ) = 3 a x 2 + 2 b x + c
Die Bedingungen, die man aus der Zeichnung herauslesen kann sind:
f ( 0 ) = 0
f ( 5 ) = - 0,5
f ( 10 ) = - 1,6
f ' ( 0 ) = 0
Daraus ergibt sich folgendes Gleichungssystem:
a * 0 3 + b * 0 2 + c * 0 + d = 0
a * 5 3 + b * 5 2 + c * 5 + d = - 0.5
a * 10 3 + b * 10 2 + c * 10 + d = - 1.6
3 a * 0 2 + 2 b * 0 + c = 0
Aus der ersten Gleichung folgt sofort: d = 0 und aus der vierten Gleichung: c = 0
Es verbleibt das System:
a * 5 3 + b * 5 2 = - 0.5
a * 10 3 + b * 10 2 = - 1.6
<=>
125 a + 25 b = - 0.5
1000 a + 100 b = - 1.6
erste Gleichung = erste Gleichung * 4 (Vorbereitung des Additionsverfahrens):
<=>
500 a + 100 b = - 2
1000 a + 100 b = - 1.6
Additionsverfahren: zweite Gleichung = zweite Gleichung - erste Gleichung
<=>
500 a + 100 b = - 2
500 a = 0,4
den Wert 0,4 für 500 a in die erste Gleichung einsetzen, zweite Gleichung durch 500 dividieren:
<=>
0,4 + 100 b = - 2
a = 0,4 / 500
<=>
100 b = - 2,4
a = 0,8 / 1000
<=>
b = - 2,4 / 100 = - 0,024
a = 0,0008
Die berechneten Werte für die Parameter a, b, c und d werden nun in die allgemeine Funktionsgleichung (siehe oben) eingesetzt. Dadurch erhält man die gesuchte konkrete Funktion:
f ( x ) = 0,0008 x 3 - 0,024 x 2
Hier ein Schaubild des Graphen dieser Funktion:
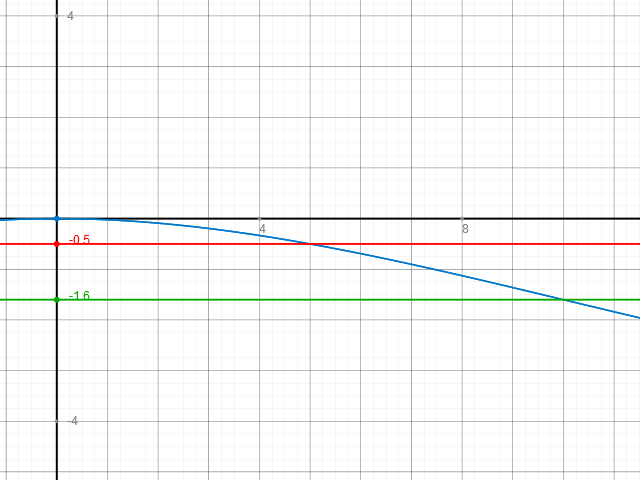
Neben dem eigentlichen Funktionsgraphen in blau habe ich noch die beiden Geraden y = - 0,5 und y = - 1,6 eingezeichnet, damit man die Funktionswerte an den Stellen x = 5 und x = 10 besser ablesen und mit der Vorgabe vergleichen kann.