Parabelgleichung aufstellen; im Koordinatensystem der Flugbahn skizzieren. Freistoss im Fussball.

Question

bei einem freistoß liegt ein fußball-horizontal gemessen-50 m weit.

der höchste punkt seiner parabelförmigen flugbahn liegt 5 m hoch.

a) als erstes brauche ich die Skizzierung der Flugbahn in einem koordinatensystem

b) und als zweites muss ich die koordinaten des scheitels und die parabelgleichung bestimmen

Answer 1

a) skizze  ist weiter unten

b) man findet inder Bescheibung drei punkte zur Bestimmung der Parabelgleichung, durch die flugbahn ergibt sich eine nach unten geöffnete Parabel

 ersten startet der Ball  in (0|0) und landet (50|0)  , der Höchste Punkt der scheitelpunkt  s(25|5) ind die normalform einsetzen

 0= a*0+b*0+c   c=0

 0=a*2500+50b        b=--50a    unten einsetzen

 5=a*625+25b           5=625a-25*(50a)

                                 5=625a-1250a

                                 5=-625a     ⇒    a=-1/125

                                                           b=2/5

f(x) = -1/125 x²+2/5 x

 

 

Answer 2

Zunächst könnte man sich eine Skizze machen und den Scheitelpunkt mit S(Sx | Sy) und einen weiteren Punkt P(Px | Py) einzeichnen.

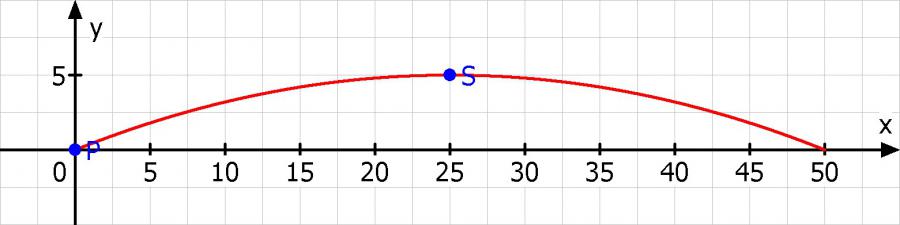
P(0 | 0) ; S(25 | 5)

Nun berechnet man den Öffnungsfaktor mit

a = (Py - Sy) / (Px - Sx)^2 = (0 - 5) / (0 - 25)^2 = -5/625 = -1/125

Nun stellt man die Scheitelpunktform auf

f(x) = a*(x - Sx)^2 + Sy = -1/125*(x - 25)^2 + 5

Man kann die Funktionsgleichung noch ausmultiplizieren und in allgemeiner Form schreiben. Dies würde ich aber nur machen, wenn es in der Aufgabenstellung ausdrücklich erwünscht ist. Ansonsten lässt man die Scheitelpunktform einfach stehen.

Nach diesem Schema ist das meist am einfachsten zu lösen.