Von einem Quader sind gegeben a, b, c. Berechne α und β. Bestimme den exakten Wert von tan 60°

Question

3. Von einem Quader sind gegeben:
\( a=6 \mathrm{~cm} \)
\( b=5 \mathrm{~cm} \)
\( c=3 \mathrm{~cm} \)

Berechne \( \alpha \) und \( \beta \).

4. Bestimme den exakten Wert von \( \tan 60^{\circ} \).

Lösung Nr. 3 - alpha: 138,0° und beta: 53,3°
Lösung Nr. 4 - ist 3

Answer 1

zu 3 )

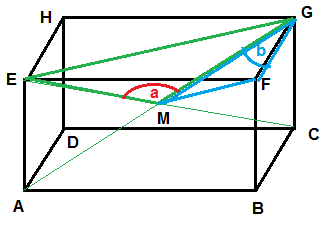
Berechnung des Winkels α (in der Skizze mit a bezeichnet)

Betrachte das grüne Dreieck EMG. Dessen Seiten sind die halben Raumdiagonalen EM und MG sowie die Flächendiagonale EG. Für den gesuchten Winkel α bei Punkt M gilt daher nach dem Kosinussatz:

EG ² = EM ² + MG ² - 2 * EM * MG * cos ( α )

<=> cos ( α ) = ( EG ² - EM ² -  MG ² ) / ( - 2 * EM * MG ) = ( EM ² +  MG ² - EG ² ) / ( 2 * EM * MG )

<=> α = arccos ( ( EM ² +  MG ² - EG ² ) / ( 2 * EM * MG ) )

Die Längen der Strecken EG, EM und MG lassen sich mit Hilfe des Satzes des Pythagoras aus den Angaben berechnen. Es ist:

EG = √ ( a ² + b ² ) = √ ( 36 + 25 ) = √ ( 61 )  [Flächendiagonale]

EM = MG = 0,5 * √ ( a ² + b ² + c ² ) = 0,5 * √ ( 36 + 25 + 9 ) = 0,5 * √ ( 70 )  [halbe Raumdiagonale]

Einsetzen in die blau gesetzte Formel ergibt:

α = arccos ( ( EM ² +  MG ² - EG ² ) / ( 2 * EM * MG ) )

= arccos ( ( 0,25 * 70 + 0,25 * 70 - 61 ) / ( 2 * 0,5 * √ ( 70 ) * 0,5 * √ ( 70 ) ) )

= arccos ( ( 35 - 61 ) / 35  ) ≈ 138 °

 

Berechnung des Winkels β (in der Skizze mit b bezeichnet)

Betrachte das blaue Dreieck FMG. Dessen Seiten sind die halben Raumdiagonalen FM und MG sowie die Quaderkante FG. Für den gesuchten Winkel β bei Punkt G gilt daher nach dem Kosinussatz:

FM ² = FG ² + MG ² - 2 * FG * MG * cos ( β )

<=> cos ( β ) = ( FM ² - FG ² -  MG ² ) / ( - 2 * FG * MG ) = ( FG ² +  MG ² - FM ² ) / ( 2 * FG * MG )

<=> β = arccos ( ( FG ² +  MG ² - FM ² ) / ( 2 * FG * MG ) )

und wegen MG = FM (halbe Raumdiagonalen) verkürzt sich der Ausdruck au f der rechten Seite zu:

<=> β = arccos ( FG ² / ( 2 * FG * MG ) )

Das kann man noch kürzen und erhält:

<=> β = arccos ( FG / ( 2 * MG ) )

 

Die Längen der Strecke MG lässt sich mit Hilfe des Satzes des Pythagoras aus den Angaben berechnen, die Länge der Strecke FG ist gegeben ( FG = 5 cm ).
Es ist:

MG = 0,5 * √ ( a ² + b ² + c ² ) = 0,5 * √ ( 36 + 25 + 9 ) = 0,5 * √ ( 70 )  [halbe Raumdiagonale]

Einsetzen in die violett gesetzte Formel ergibt:

β = arccos ( FG / ( 2 * MG ) )

= arccos ( 5 / ( 2 * 0,5 * √ ( 70 ) )

= arccos ( 5 /  √ ( 70 ) ) ≈ 53,3 °

 

zu 4)

Wie dir jeder vernünftige Taschenrechner sagen wird, ist

tan ( 60 ° ) = 1,73205... = √ ( 3 )

nicht 3.

Man rechnet:

tan ( 60 ° ) = sin ( 60 ° ) / cos ( 60 ° )

Die Werte von sin ( 60 ° ) = 0,5  * √ ( 3 ) und cos ( 60 ° ) = 0,5 sollte man kennen, also:

= 0,5 * √ ( 3 ) / 0,5

= √ ( 3 )