ja, einen solchen Weg gibt es, und er ist extrem einfach; wir konstruieren ein Steigungsdreieck:
Du subtrahierst den y-Wert des Punktes, der weiter links liegt - also hier (-1|4) - vom y-Wert des Punktes, der weiter rechts liegt - also hier (3|4)
und dividierst diese Differenz durch die Differenz der entsprechenden x-Werte.
Insgesamt erhältst Du in diesem Beispiel also eine Steigung von
(4 - 4) / (3 -(-1)) =
(4 - 4) / (3 + 1) =
0/4 =
0
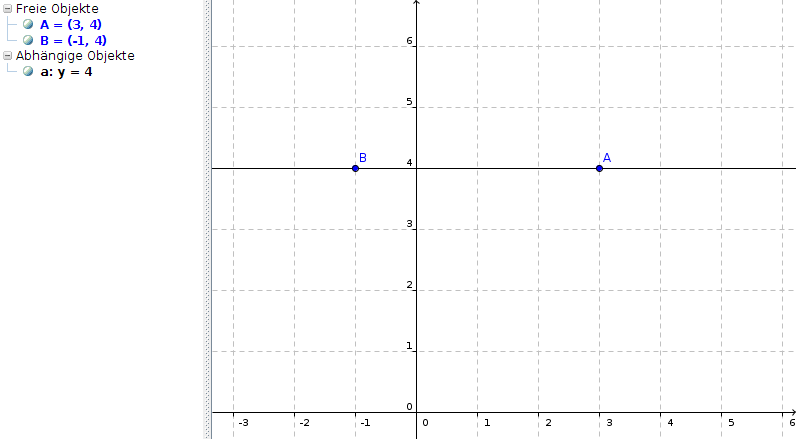
Und die Gerade durch die beiden gegebenen Punkte hat ja tatsächlich die Steigung 0:
Besten Gruß