Question

Skizziere die folgenden Teilmengen in der komplexen Ebene:

1)      {z ∈ ℂ | |z - 1 - 2i| ≤ 1},

2)      {z ∈ ℂ | Re(iz) > 0},

3)      {z ∈ ℂ | Re(z²) > 0},

4)      {xe^ix | x ∈ ℝ_≥0}.

Answer 1

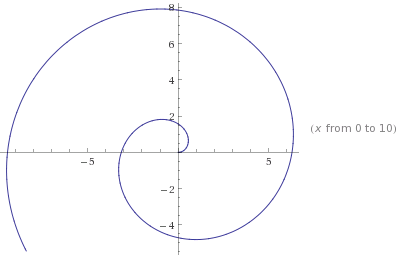
1)      {z ∈ ℂ | |z - 1 - 2i| ≤ 1},

|x + yi - 1 - 2i| ≤ 1
|i·(y - 2) + x - 1| ≤ 1
(y - 2)^2 + (x - 1)^2 ≤ 1

 

2)      {z ∈ ℂ | Re(iz) > 0},

Re(i * (x + yi)) > 0
Re(xi - y) > 0
- y > 0
y < 0
Alles unterhalb der x-Achse

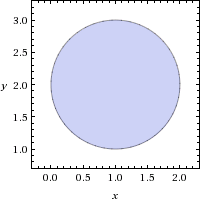
3)      {z ∈ ℂ | Re(z²) > 0},

Re((x + yi)^2) > 0
Re(x^2 + 2·i·x·y - y^2) > 0
x^2 - y^2 > 0

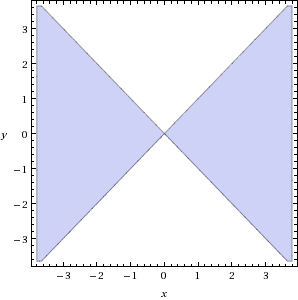
4)      {xe^ix | x ∈ ℝ_≥0}.

Comments

Vielen vielen Dank. Noch eine Frage: Wie kommt man von

|i·(y - 2) + x - 1| ≤ 1

auf
(y - 2)² + (x - 1)² ≤ 1  ?

Kann man Klammern beliebig setzten und beliebig quadrieren? Ginge theoretisch auch

(y - 2) +  (x - 1)   ≤ 1 ? Also ohne quadrieren?

---

Wie ist der Betrag einer komplexen Zahl z definiert ?

|z| = |x + yi| = ???

Wenn du es nicht weißt schau unter --> https://de.wikipedia.org/wiki/Komplexe_Zahl

---

Ok, tut mir leid. Dummer Fehler meinerseits. Aber nochmals vielen Dank.