Elementarmatrizen. Elementaroperationen: Bsp. E3 (Addition der mit k multiplizierten j-ten Zeile zur i-ten Zeile)

Question

Stellen Sie für eine (3x3)-Matrix Beispiele für die drei sog. Elementarmatrizen vor, welche die Elementaroperationen E1 (Zeilenvertauschung i gegen j), E2 ( Multiplikation der i-ten- Zeile mit der Zahl k ≠ 0) und E3 (Addition der mit k multiplizierten j-ten Zeile zur i-ten Zeile) ausführen.

Answer 1

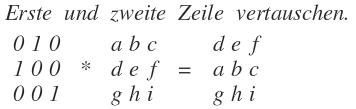
Erste\quad und\quad zweite\quad Zeile\quad vertauschen.\\ \begin{matrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{matrix}\quad *\quad \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\quad =\quad \begin{matrix} d & e & f \\ a & b & c \\ g & h & i \end{matrix}

Analog (erste und dritte) oder (zweite und dritte) Zeile vertauschen.

 

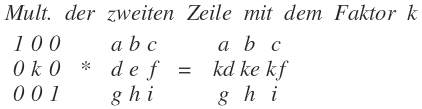
Mult.\quad der\quad zweiten\quad Zeile\quad mit\quad dem\quad Faktor\quad k\\ \begin{matrix} 1 & 0 & 0 \\ 0 & k & 0 \\ 0 & 0 & 1 \end{matrix}\quad *\quad \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\quad =\quad \begin{matrix} a & b & c \\ kd & ke & kf \\ g & h & i \end{matrix}

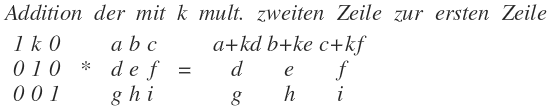
Addition\quad der\quad mit\quad k\quad mult.\quad zweiten\quad Zeile\quad zur\quad ersten\quad Zeile\\ \begin{matrix} 1 & k & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}\quad *\quad \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\quad =\quad \begin{matrix} a+kd & b+ke & c+kf \\ d & e & f \\ g & h & i \end{matrix}

Die restlichen Matrizen, mit denen hier mult. werden muss, kann man analog konstruieren.