Gib den Funktionsterm einer quadratischen Funktion an und x^4 = 12 – x^2

Question

Hallo vielleicht kann mir jemand weiterhelfen, denn ich verzweifle an quadratischen Funktionen Aufgabe:

Löse die Gleichung  x⁴ = 12 - x²  
ich weiß dass die Formel  x 1/2= -b +/ -  wurzel aus b hoch2 - 4ac durch 2a ist
aber wie rechne ich denn das mit x⁴???  

zweite Frage a) Gib den Funktionsterm einer quadratischen Funktion an, deren kleinster Funktionswert -9 ist und deren Nullstellen bei -1 und +2 liegen.  

Meine Lösung -9(x-1)+2  nachdem ich dies wahrscheinlich falsch habe konnte ich die aufgabe b nicht lösen :

b) Liegt der Punkt P(-2,5/5,75)auf dem Graphen von f?

Bitte um Hilfe Danke

Comments

b) Eine Parabelgleichung sollte eigentlich irgendwo ein Quadrat haben. Wo ist das in deiner Lösung?

Eine Kurzversion von dem, was bei a) zu tun ist, findest du in der Antwort zu a) bei folgender Frage:

https://www.mathelounge.de/8096/gegeben-ganzrationale-funktion-gesucht-nullstellen-symmetrie

---

Vielen Dank für deine Antwort häng jetzt momentan ganz schön

wenn ich die Gleichung auflöse muss ich die x hoch 4 auf die andere Seite bringen damit ich 0= ... herausbekomme?

 

hier noch eine die ich gar nicht kapiere: Skizziere die Parabeln indem du die Funktionsterme zunächst auf Scheitelpunktform bringst.

f(x)= -xhoch2 + 6x -9   meine Lösung   -x(x-3)hoch2 -9

---

wenn ich die Gleichung auflöse muss ich die x hoch 4 auf die andere Seite bringen damit ich 0= ... herausbekomme?

ja genau. und dann z=x^2 setzen.

Mit deiner Formel z berechnen. Nachher ±Wurzel aus diesen Zahlen berechnen. Das sind dann die maximal 4 Lösungen der gegebenen Gleichung.

Deine Lösung zur Zusatzfrage ist wieder unmöglich. Du hast ja da mit x und x^2 eigentlich x^3 drinn.  

f(x)= -x² + 6x -9 = - (x^2 - 6x + 9) = - (x-3)^2 +0 ist die gesuchte Scheitelpunktform.

S(3, 0)

Nachtrag:

(x^2 - 6x + 9) ist ein Binom (x-3)^2

Nun darfst du die Funktion nicht verändern, musst aber + irgendetwas haben. Das geht nur, wenn du +0 schreibst.

Answer 1

 

Zur zweiten Frage a) Gib den Funktionsterm einer quadratischen Funktion an, deren kleinster Funktionswert -9 ist und deren Nullstellen bei -1 und +2 liegen.  

Meine Lösung -9(x-1)+2  nachdem ich dies wahrscheinlich falsch habe konnte ich die aufgabe b nicht lösen :

 

Damit eine Funktion die angegebenen Nullstellen hat, müssen diese als sog. Linearfaktoren in der Funktionsgleichung auftauchen.

Also Ansatz: f(x) = a(x+1)(x-2)

Jetzt muss man noch den kleinsten Funktionswert -9 einbeziehen.

Dieser wird aus Symmetriegründen genau zwischen den beiden Nullstellen angenommen. Also bei x_s = 0.5 (-1 + 2) = 0.5

f(0.5) = a(1.5)(1.5) = a*2.25 = -9

a = -9/2.25 = -4

Somit f(x) = -4 (x+1)(x-2) =- 4(x^2 - x - 2) = -4x^2 + 4x + 8

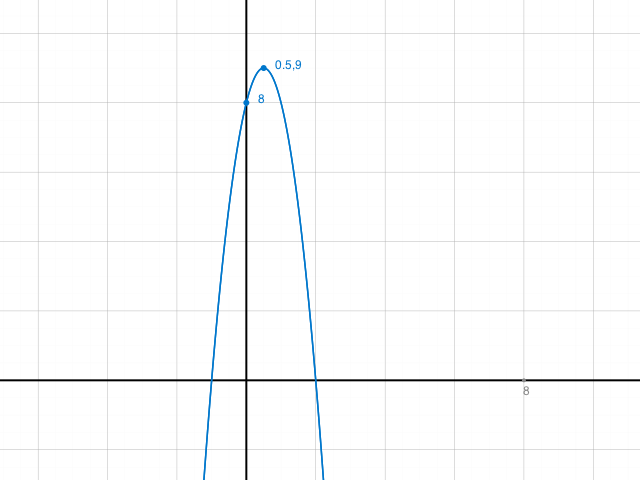
Kontrolle: Graph. Nun kannst du b) bestimmt selbst lösen.

 

Comments

Hallo Frage: wie komme ich bei S(3,0) auf die 0 (in blau) Danke

---

Kommentar gehört zum Kommentar zur Frage. Antwort hab ich dort ergänzt.

Stell bitte neue Fragen nicht in den Kommentaren der andern. Das gibt einen Salat. Du kannst ja neue (andere!) Fragen stellen.

Answer 2

zu eins : wenn man die Gleichung umstellt erhält man

0=-x⁴-x²+12    |

0=-1*(x⁴+x²-12)           |Faktorisieren

0=-(x²-3)*(x²+4) 

aus x²-3   ergibt sich dass     x²=3    dann ist x_1,2=±√3

aus x²+4  ergibt sich dass     x²=-4   dann ist  x_3,4= ±√-4     oder ±2i

Man könnte narürlich auch substituieren uns x²=z und x⁴⁼z² setzen uns dnn die pq-Formel anwenden und dann zurücksubstituiren.