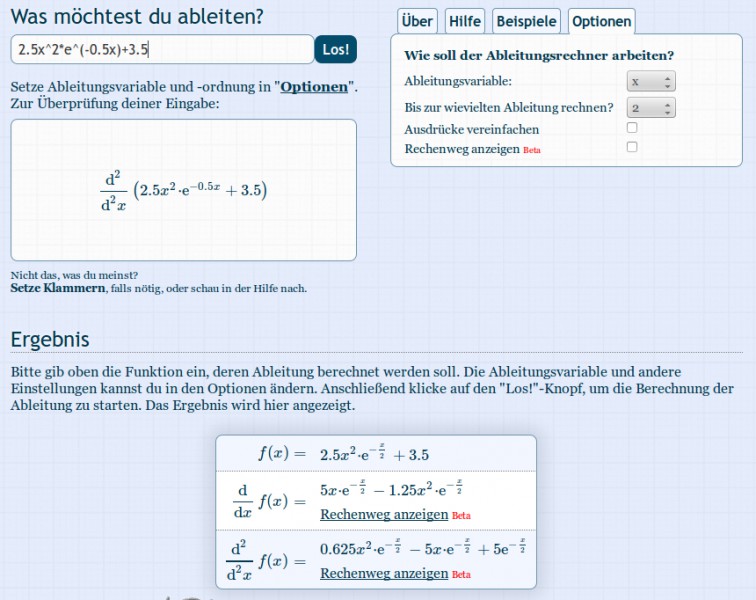
Produktregel:
(uv)' = u'v + uv'
u = 2,5t2
u' = 5t
v = e-0,5t
Nun mit äußerer und innerer Ableitung
v' = -0,5 * e-0,5t
Insgesamt:
h'(t) = 5t * e-0,5t + 2,5t2 * (-0,5) * e-0,5t = (5t - 1,25t2) * e-0,5t
Wieder Produktregel:
u = (5t - 1,25t2)
u' = 5 - 2,5t
v = e-0,5t
v' = -0,5 * e-0,5t
Insgesamt:
h''(t) = (5 - 2,5t) * e-0,5t + (5t - 1,25t2) * (-0,5) * e-0,5t = (5 - 2,5t - 2,5t + 0,625t2) * e-0,5t = (5 - 5t + 0,625t2) * e-0,5t
Besten Gruß