man kann das Abbrennen der beiden Kerzen mit zwei linearen Gleichungen der Form y = mx + b beschreiben und dann deren Schnittpunkt berechnen:
Kerze A:
y = -2,4x + 35,5
Sie ist anfangs 35,5cm lang und wird je Stunde x um 2,4cm kürzer
Kerze B:
y = -1,1x + 14,7
Wir setzen die beiden Gleichungen gleich und erhalten:
-2,4x + 35,5 = -1,1x + 14,7 | + 2,4x
35,5 = 1,3x + 14,7 | - 14,7
20,8 = 1,3x | : 1,3
x = 16
Nach 16 Stunden haben die beiden Kerzen die gleiche Länge:
Probe
Kerze A: 35,5cm - 16 * 2,4cm = -2,9cm
Kerze B: 14,7cm - 16 * 1,1cm = -2,9cm
Diese Lösung ist natürlich nicht befriedigend, ich sehe aber keinen Fehler in obiger Berechnung. Der "Vorsprung" der Kerze B scheint trotz des langsameren Abbrennens einfach zu groß zu sein:
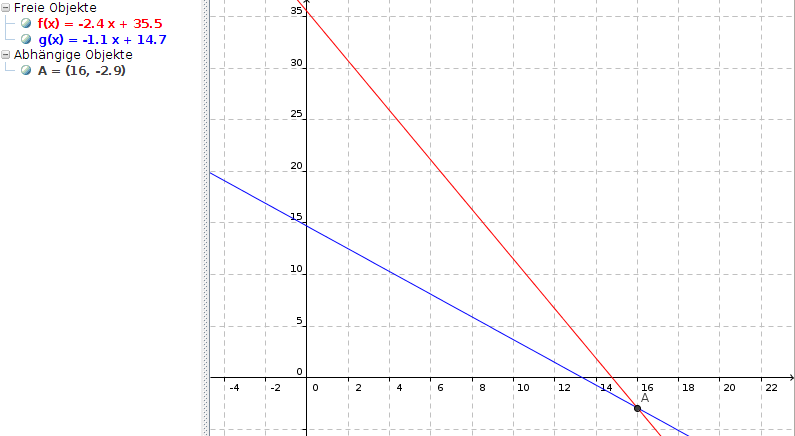
Habe ich falsch gerechnet? Dann bitte melden :-D
Besten Gruß