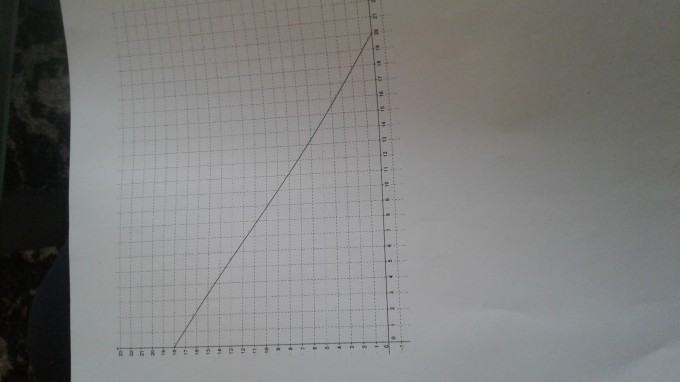
Es werden zwei unterschiedliche Kerzen betrachtet. Die Kerzen sind zylinderförmig. Beide Kerzen werden gleichmäßig angezündet. Dabei lässt sich die jeweilige verbleibende Kerzenhöhe y (in cm) in Abhängigkeit von der Brenndauer x (in Stunden) als Abbrenfunktion beschteiben. Das Schaubild in der Anlage zeigt, wie Kerze 1 gleichmäßig anbrennt.
Kerze 1 Kerze 2
A)Gib mithilfe dieser Grafik an:
-die Höhe der Kerze 1 vor Beginn des Abbrennvorgangs und
-die Dauer des Abbrennvorgangs bis zum vollständigen Abbrennen der Kerze.
Kerze 2 ist zum Zeitpunkt des Anzündens 20 cm hoch. Nach zwei Stunden ist sie um 3 cm kürzer.
B)Zeichne den Graphen der Abbrenfunktion für die Kerze 2 in das Koordinatensystem in der Anlage und gibt an, zu welchem Zeitpunkt die Kerze vollständig abgebrannt ist.
C)Gib mithilfe der graphischen Darstellungen den Zeitpunkt an, zu dem Kerze 1 und Kerze 2 gleich hoch sind.
D)Begründe, warum die Graphen der Abbrenfunktionen der beiden Kerzen linear sind.
E)Bestimme die Gleichung der Abbrenfunktion von Kerze 1. Bestimme mithilfe dieser Gleichung dir Brenndauer der Kerze 1, bis sie nur noch 8 cm hoch ist.