Bestimmen Sie die Koordinaten bezüglich des affinen Koordinatensystems K' = (A, AD, AB).

Question

In einem kartesischen Koordinatensystem K der euklidischen Ebene E² ist eine Raute (gleichseitiges Viereck) ABCD gegeben. Die Länge der Diagonalen AC betrage 4, die Diagonale BD sei 6 lang. 

Sei P der Punkt mit dem Koordinatenvektor p=(-2   3)^T bezüglich K. Bestimmen Sie die Koordinaten von P bezüglich des affinen Koordinatensystems K^' = (A, AD, AB).

Wie muss ich jetzt vorgehen? 

Comments

War da eventuell eine Skizze bei? Weil ich so ja gar nicht weiß wie die Raute im Koordinatensystem liegt.

---

Ja, da war eine Skizze dabei. Aber ich wusste nicht, wie ich die Skizze hier zeichnen soll.

---

Hier ist die Zeichnung ;)

Answer 1

Am einfachsten machst du das direkt in der Skizze.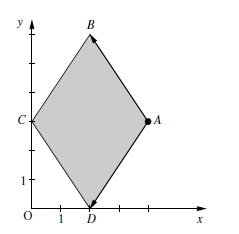

Ergänze die negativen Bereiche des Koordinatensystems und den Punkt P(-2|3).

Nun kannst du das Koordinatengitter des neuen Koordinatensystems darüberlegen.

Dazu verlängerst du

1. AD gegen unten und trägst AD ein paar mal ab. Beschrifte A mit 0, D mit 1 fahre weiter mit 2,3,4... Das ist dann die neue x-Achse

2. AB gegen oben und trägst AB ein paar mal ab. Beschrifte A mit 0, B mit 1 fahre weiter mit 2,3,4... DAs ist nun die neue y-Achse. 

3. Koordinatengitter ergänzen (lauter Rauten).

4. Idealerweise liegt P gerade auf einem Rauteneckpunkt und du kannst seine Koordinaten entlang der neuen Gitterlinien gleich ablesen.

Comments

Dankeschön. Aber gibt es auch andere Herangehensweisen? Brauch ich überhaupt keine Rechnung?

---

Warum willst du denn rechnen, wenn du's ablesen kannst?

Wenn du unbedingt rechnen willst, löse die Vektorgleichung

0P = (0A) + k*(AD) + m (AB) nach den reellen Parametern k und m auf.

k ist die neue x-Koordinate

m die neue y-Koordinate.