Wann ist die Fläche des Dreiecks minimal? Eine Ecke beweglich auf Graph von y=x^2-6x+13

Question

Aufgabe:

a) Zeichnen Sie in Geogebra den Graphen \( f(x)=x^{2}-6 x+13 \) und einen beweglichen Punkt A auf diesem Graphen. Bilden Sie ein Dreieck aus den Punkten A, B mit den Koordinaten \( (0 | 4), \) C mit den Koordinaten \( (4 | 0) . \) Bestimmen Sie mit Geogebra den Flächeninhalt des Dreiecks und untersuchen Sie, wie der Flächeninhalt sich je nach Lage von A verändert. Schreiben Sie Ihre Vermutung auf und dokumentieren Sie Ihre Vorgehensweise.

b) Für welches \( x \) ist der Flächeninhalt des Dreiecks minimal? Begründen Sie!

Ansatz:

a habe ich, ich brauche hilfe bei b. Wie kann ich zeigen, dass die Fläche minimal ist. Vielleicht so? f(x)*x*1/2=0 dann die notwendige und hinreichende Bedingung. Aber wir sollen den Flächeninhalt des Dreiecks bestimmen, weshalb ich meine dass es so nicht geht.

Answer 1

 

Dies müßte die Skizze sein. Die Achsen sind allerdings nicht gleich skaliert
was aber keine Rolle spielt.

Eine Seite des Dreiecks ist die Gerade B nach C ( 0 | 4 ) nach ( 4 | 0 ).
Punkt  A liegt auf der blauen Kurve.
Die Fläche des Dreiecks berechnet sich nach Grundlinie mal Höhe * 1/2
Strecke BC mal ( Abstand A zur LInie BC.)
Verschiebe ich jetzt die Linie BC parallel nach oben ist der Berührpunkt
A der kleinste Abstand oder die kleinste Höhe.
Die verschobene Linie ist eine Tangente im Punkt A.
Sie hat dieselbe Steinung wie die blaue Kurve.
Steigung der Strecke BC = -1
f ( x ) = x^2 - 6 * x + 13
f ´( x ) = 2 * x - 6
Im Punkt A
2 * x - 6 = -1
2 * x = 5
x = 2.5

Dies müßte die Antwort auf Frage b.) sein.

Bei Fehlern oder Fragen wieder melden.

mfg Georg

Comments

Whow. Klasse gelöst. Das ist ja noch viel einfacher als mein Weg.

Answer 2

Sind Grundkenntnisse der Vektorrechnung vorhanden? Dann könnte man das wohl recht geschickt über das Kreuzprodukt lösen.

BC = [4, 0] - [0, 4] = [4, -4]

BA = [x, x^2 - 6·x + 13] - [0, 4] = [x, x^2 - 6·x + 9]

Gerichtete Fläche

A = 1/2 * BC * BA = 1/2·ABS([4, -4] ⨯ [x, x^2 - 6·x + 9]) = 2·x^2 - 10·x + 18

A' = 4·x - 10 = 0
x = 2.5

A(2.5) = 5.5

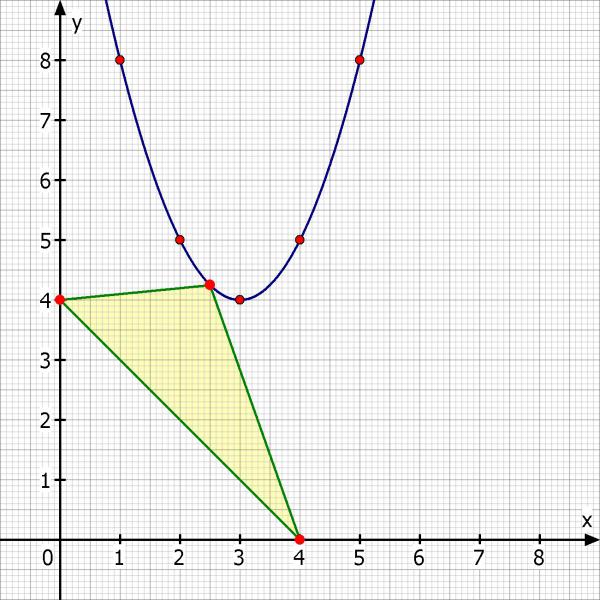
Skizze:

Answer 3

A = 1/2 * g * h

g ist Grundseite des Dreiecks. Funktionsgleichung g(x)= -x

Länge g=const., da feste Punkte vorgegeben

Entscheidend ist h.

h ist minimal, wenn es senkrecht auf f(x) auftrifft.

Somit muss die STEIGUNG von g(x) gleich der STEIGUNG von  f(x) sein. Parallelen !

g'(x)= -1

f'(x)= 2x-6

g'(x) = f'(x)

-1 = 2x -6

x=2,5