Question

Für welche Parameterwerte c gibt es reelle Lösungen x zu x^2+cx+c=0?

Answer 1

x² + cx + c = 0

Die Diskriminante sollte >= 0 sein

(p/2)^2 - q = c^2/4 - c = c^2/4 - 4c/4 = (c^2 - 4c)/4 >= 0

c^2 - 4c >= 0
c(c - 4) >= 0

c <= 0 oder c >= 4

Comments

@Mathecoach:

Wenn c = 2, dann gilt c ≥ 1

Also

x² + 2x + 2 = 0

x_1,2 = -1 ± √(1-2)

=> Keine reelle Lösung.

 

Dein Fehler liegt wohl hier:

c²/4 - 4c/4 = (c² - c)/4

 

Lieben Gruß

Andreas

---

Ja. Da gehört natürlich noch eine 4 in die Klammer.
Danke für die Verbesserung.

---

Keine Ursache.

Answer 2

 

x² + cx + c = 0

pq-Formel

x_1,2 = -c/2 ± √(c²/4 - c)

Reelle Lösungen gibt es dann, wenn der Ausdruck unter der Wurzel ≥ 0 ist.

c²/4 - c ≥ 0 | * 4

c² - 4c ≥ 0 | +4c

c² ≥ 4c

c * c ≥ 4 * c | : c

c positiv:

c ≥ 4

c negativ:

c ≤ 4

Da aber c negativ sein soll, muss es kleiner als 0 sein.

Allerdings gibt es auch eine doppelte Nullstelle für c = 0.

Reelle Lösungen gibt es also für c ≤ 0 und für c ≥ 4.

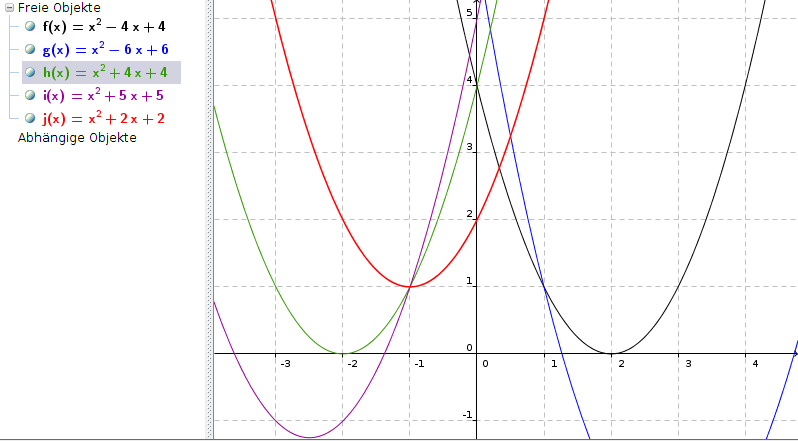
Hier ein paar Beispiel-Funktionen (davon hat nur j(x) mit c = 2 keine reelle Nullstelle, weil  0 < 2 < 4):

 

Besten Gruß